Задание №10 ОГЭ по физике

Основы термодинамики: расчетная задача

В задании № 10 ОГЭ предлагается задача без вариантов ответов. Для ее решения необходимо знание основных понятий и явлений термодинамики, а также формул, используемых для количественного определения соответствующих физ.величин. Необходимые для решения сведения приведены в разделе теории к заданию, а часть их, уже использовавшаяся для решения заданий № 8 и № 9 ОГЭ, – в теоретических разделах к этим заданиям.

Теория к заданию №10 ОГЭ по физике

Количество теплоты

Количество теплоты (Q), которое выделяется при охлаждении физ.тела либо поглощается при его нагревании, может быть вычислено так:

где c – удельная теплоемкость физ.тела, m – его масса.

∆t – это изменение температуры, которое и вызвало выделение или поглощение теплоты. При этом t1 – начальная температура, t2 – конечная. Соответственно, при отдаче теплоты ∆t будет положительной величиной, при поглощении – отрицательной. Если знак «+» или «–» учитывать в задаче не требуется, то можно просто от большего значения температуры отнимать меньшее.

Поскольку 10С=1К, то , т.е. изменение температуры может быть выражено как в градусах Цельсия (0С), так и в кельвинах (К).

Когда происходит полное сгорание (плавление, парообразование и т.д.) вещества, то количество теплоты, затрачиваемой – поглощаемой либо выделяющейся – на этот процесс, должно быть рассчитано по формуле:

где m – масса сгоревшего (расплавившегося, испарившегося и т.д.) вещества, x – удельная теплота сгорания (плавления, парообразования и т.д.). Коэффициент х обозначается как: 1) q при сгорании вещества, 2) r при парообразовании, 3) λ при плавлении.

Значение Q при этом может иметь как положительным, так и отрицательным. Для процессов, сопровождающихся выделением теплоты (например, для конденсации), Q=хm>0. Для процессов, сопровождающихся поглощением теплоты (к примеру, для плавления), Q= –хm<0.

Работа тепловой машины

Тепловая машина, или тепловой двигатель, представляет собой устройство, используемое для совершения механической работы механизмами (мотоциклами, автомобилями и др.). В самом общем виде это происходит так: в устройство подается топливо, внутренняя энергия которого преобразуется в механическую энергию. Работа при этом совершается за счет расширения газа (рабочего тела), возникающего при повышении его температуры при сгорании топлива.

Работа теплового двигателя вычисляется по формуле:

где Q1 – кол-во теплоты, выделяющейся при сгорании топлива и расходующейся на нагревание рабочего тела (т.е. кол-во теплоты нагревателя), Q2 – кол-во теплоты, отданного охлаждающей части двигателя (т.н. холодильнику). Последнее (наличие холодильника) необходимо для снижения величины работы, затрачиваемой для сжатия рабочего тела.

Коэффициент полезного действия

Коэффициент полезного действия (КПД) – это величина, показывающая эффективность функционирования механизма. КПД обозначают греческой буквой ɳ («эта»).

Вычисляется КПД так:

где Т1 – температура нагревателя, Т2 – температура холодильника.

Выражение Q1–Q2 называют полезной работой, т.е. Q1–Q2=Ап. Поэтому КПД можно выразить формулой:

где Q – кол-во теплоты, получаемой двигателем от нагревателя.

КПД выражается в процентах или в долях. Формулы, которые необходимо применять для получения результата в долях, приведены выше. Для получения КПД в процентах следует использовать уравнения:

Теоретически возможный вечный двигатель должен иметь КПД, равный 100% или 1. Но поскольку в реальности часть энергии, получаемой двигателем от сгорания топлива, расходуется на нормальное функционирование самого двигателя, то КПД любой машины всегда менее 100% (или, соответственно, меньше 1).

Уравнение теплового обмена

В изолированной системе суммарная величина кол-ва теплоты, выделяемой и поглощаемой телами этой системы, остается неизменной. Математически это выражается уравнением:

где Q1, Q2,…,Qn – кол-ва теплоты, отдаваемые физ.телами системы в процессе их взаимодействия в этой системе, Q1’, Q2’,…,Qn’ – кол-ва теплоты, поглощаемые физ.телами системы.

Приведенное равенство называют ур-нием теплового обмена. Это уравнение является, по сути, проявлением в термодинамике з-на сохранения энергии.

Разбор типовых вариантов заданий №10 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

На рисунке представлен график зависимости температуры t твёрдого тела от полученного им количества теплоты Q. Масса тела 2 кг. Чему равна удельная теплоёмкость вещества этого тела?

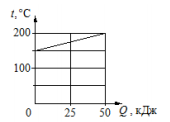
Ответ: ___________________________ .

[/su_note]

Алгоритм решения:
  1. Записываем формулу для вычисления кол-ва теплоты. Выражаем из нее уд.теплоемкость (искомую величину).
  2. Используя приведенный в условии график, определяем изменение темп-ры ∆t и кол-во теплоты Q, необходимые для вычисления с.
  3. Используя данные, полученные в п.2 и значение для массы тв.тела, данное в условии, находим с.
Решение:
  1. Из формулы для кол-ва теплоты 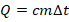 уд.теплоемкость с равна: .
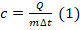  2. Согласно приведенному графику, всего было получено кол-во теплоты 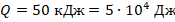. При этом температура ∆t изменилась на: 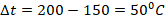. Масса по условию:  .
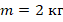  3. Подставим данные из п.2 в (1). Получим: .

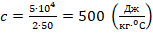Ответ: 500

Первый вариант (Камзеева, № 5)

[su_note note_color=»#defae6″]

Какое минимальное количество керосина надо налить в примус для нагревания 1 л воды от начальной температуры  до температуры кипения? Пренебречь потерями энергии и теплоемкостью чайника. Ответ округлить до десятых.

Ответ: _______ г

[/su_note]

Алгоритм решения:
  1. Записываем табличные данные, необходимые для решения задачи. Переводим в СИ значение объема воды и находим соответствующую ему массу.
  2. Записываем уравнение для нахождения кол-ва теплоты, которое получит вода для ее доведения до темп-ры кипения (1).
  3. Записываем формулу для определения кол-ва теплоты, необходимого для сгорания керосина (2). Объединяем (1) и (2), выражаем из полученного уравнения искомую массу.
  4. Определяем искомую массу керосина.
Решение:
  1. Темп-ра кипения воды составляет: 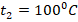. Уд.теплоемкость воды: 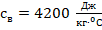. Уд.теплота сгорания керосина: 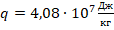. Темп-ра кипения воды: tк=100 0С. Объем воды: 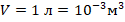; отсюда масса воды .
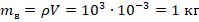  2. Кол-во теплоты, которую получит вода для достижения темп-ры кипения, равно: .
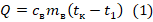  3. При сгорании керосина выделится кол-во теплоты, равное: Q=qmк (2). Поскольку вся энергия (теплота), выделяющаяся при сгорании керосина, расходуется для нагрева воды, то (1)=(2). Тогда получим: .
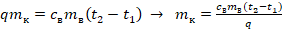  4. Вычисляем массу керосина: 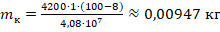. Поскольку требуется представить ответ в граммах, округлив его до десятых, то переведем результат соответственно: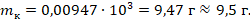

Ответ: 9,5

Второй вариант (Камзеева, № 7)

[su_note note_color=»#defae6″]

Двигатель мотоцикла сжигает 20 г бензина, совершая при этом полезную работу 184 кДж. Чему равен коэффициент полезного действия двигателя? Ответ округлите до целого.

Ответ: ____%

[/su_note]

Алгоритм решения:
  1. Записываем табличное значение для уд.теплоты сгорания бензина, которое необходимо для решения задачи. Переводим в СИ данные из условия.
  2. Записываем уравнение для вычисления КПД (1).
  3. Определяем формулу для расчета Q – кол-ва теплоты, получаемой двигателем от сгорания бензина (2). (2) → (1).
  4. Вычисляем искомую величину.
Решение:
  1. Уд.теплота сгорания бензина: 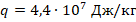. Масса бензина: m=20 г=0,02 кг. Полезная работа: .
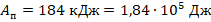  2. КПД двигателя равен: .
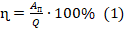  3. Q можем найти из формулы: Q=qm (2). Подставим (2) в (1): .
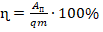  4. Найдем КПД: 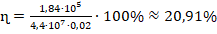. Поскольку в условии требуется округлить результат до целых, то получим: ɳ=20,91 %≈21 %.

Ответ: 21

Третий вариант (Камзеева, № 13)

[su_note note_color=»#defae6″]

Смешали две порции воды: 1,6 литра при температуре t1=25 0C и 0,4 литра при t2=100 0С. Определите температуру получившейся смеси. Теплообменом с окружающей средой пренебречь.

Ответ: ____ 0С.

[/su_note]

Алгоритм решения:
  1. Определяем кол-во теплоты для воды с начальной темп-рой t1.
  2. Определяем кол-во теплоты для воды с нач.температурой t2.
  3. Используем ур-ние теплового обмена и выражаем из него искомую величину.
  4. Находим искомую величину.
Решение:
  1. Вода с нач.температурой t1=25 0C при смешении с водой при более высокой темп-ре (здесь – при 100 0С) будет нагреваться. После нагрева и достижения теплового равновесия ее темп-ра станет равной t. В процессе нагревания вода поглотит кол-во теплоты, равное: .
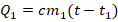  2. Вода с нач.температурой t2=100 0С при соединении с водой более низкой темп-ры (в данном случае – при 25 0С) начинает охлаждаться. В результате охлаждения эта вода достигнет состояния теплового равновесия и, соответственно, температуры t. При таком охлаждении вода отдаст кол-во теплоты, равное: .
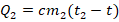  3. Используя ур-ние теплового обмена, получим: 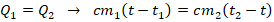. Выполним преобразования:  .
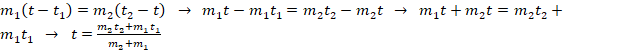  4. Значения кол-ва воды из литров в кг переводить не будем, поскольку из итоговой формулы видно, что 10-3, на величину которого потребовалось бы для этого домножить каждое из m, при расчете все равно сокращаются. Поэтому: .

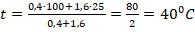Ответ: 40

Текст: Базанов Даниил, 5k 👀