Задание №11 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Задание №11 ЕГЭ по физике продолжает тему термодинамики и молекулярно-кинетической теории.
Задание ЕГЭ-Ф-ДВ2023-9
Алгоритм решения:
- Записать исходные данные.
- Записать формулу, отображающую зависимость между работой, внутренней энергией газа и количеством теплоты, полученным этим газом.
- Подставить известные величины и сделать вычисления.
Решение:
Запишем исходные данные:
- Количество теплоты, сообщенное газы: Q = 300 Дж.
- Изменение внутренней энергии газа: ∆U = 100 Дж.
Зависимость между работой, внутренней энергией газа и количеством теплоты, полученным этим газом, устанавливает первое начало термодинамики:
–∆U = Q – A
Перед изменением внутренней энергией газа ставим знак «минус», так как в результате совершения описанного процесса внутренняя энергия газа уменьшилась. Перед количеством теплоты ставим знак «плюс», так как газу сообщили это количество теплоты. Перед работой ставим знак «минус», так как газ совершает ее. Следовательно, газ совершил работу:
A = Q + ∆U = 300 + 100 = 400 (Дж)
Ответ: 400pазбирался: Алиса Никитина | обсудить разбор
Задание EF18139
Паук-серебрянка медленно спускается на дно равномерно прогретого озера, неся между волосками брюшка пузырьки воздуха для своего подводного жилища. Какой процесс происходит с воздухом в пузырьках по мере погружения паука?
Ответ:
а) изобарное сжатие
б) изохорное нагревание
в) изотермическое сжатие
г) адиабатное сжатие
Алгоритм решения
- Установить, какие величины меняются по мере погружения пузырьков воздуха на глубину.
- Выяснить, какие величины сохраняются постоянными.
- Установить вид изопроцесса.
Решение
Когда паук спускается в воде на глубину, давление постепенно увеличивается. На пузырьки воздуха будет действовать сумма атмосферного давления и давления столба воды. Под действием этого давления пузырек будет сжиматься. То есть, давление будет уменьшаться. Но само давление воздуха в пузырьке при этом будет равно давлению, оказываемому на него со стороны внешней среды. Следовательно, давление в пузырьке будет увеличиваться. При условии, что количество вещества в пузырьке при этом не меняется, величина температуры также должна оставаться постоянной. Это следует из уравнения состояния идеального газа. Следовательно, воздух в пузырьках претерпевает изотермическое сжатие.
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF17492
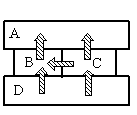 Четыре металлических бруска положили вплотную друг к другу, как показано на рисунке. Стрелки указывают направление теплопередачи от бруска к бруску. Температуры брусков в данный момент 100°С, 80°С, 60°С, 40°С. Температуру 40°С имеет брусок
Четыре металлических бруска положили вплотную друг к другу, как показано на рисунке. Стрелки указывают направление теплопередачи от бруска к бруску. Температуры брусков в данный момент 100°С, 80°С, 60°С, 40°С. Температуру 40°С имеет брусок
- A
- B
- C
- D
Алгоритм решения
- Определить тип теплопередачи.
- Вспомнить, как происходит этот тип теплопередачи.
- Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.
Решение
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.
На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 оС.
Ответ: Apазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
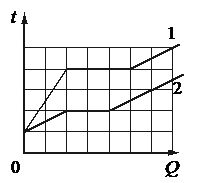 На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вдpазбирался: Алиса Никитина | обсудить разбор
Задание EF17505
 Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123pазбирался: Алиса Никитина | обсудить разбор
👀 9k