Задание №12 ОГЭ по физике

Цепи постоянного тока

В задании № 12 ОГЭ по физике необходимо понимание явления постоянного тока, процессов, протекающих в цепях постоянного эл.тока, и знание формул, описывающих такие процессы количественно. Полезные сведения, которые могут потребоваться для решения задания, приведены в разделе теории.

Теория к заданию №12 ОГЭ по физике

Сопротивление цилиндрического проводника

Цилиндрическим считается проводник, имеющий круг в поперечном сечении. Сопротивление такого проводника может быть найдено из уравнения:

где ρ – удельное эл.сопротивление, индивидуально характерное для различных материалов; l – длина проводника; S – площадь его поперечного сечения.

Последовательное и параллельное соединение проводников

Последовательное соединение:

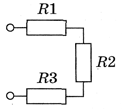
При последовательном соединении сопротивления и напряжения на каждом из резисторов суммируются. Сила тока при этом является неизменной на всех участках разветвления.

Математически это выражается формулами:

Параллельное соединение:

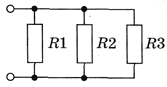
При параллельном соединении суммируются, наоборот, силы тока на каждом из участков. Неизменным при этом остается напряжение. А общее сопротивление определяется по особой формуле.

Математически это выглядит так:

Заряд в проводнике

В проводнике движутся электроны. Эл.ток возникает при их упорядоченном (т.е. направленном) перемещении с какой-то скоростью. Интерес в данном случае представляет величина заряда, который проходит через поперечное сечение данного проводника за определенное время ∆t. Вычислить эту величину можно по формуле:

Мощность электрической цепи

Эту величину можно рассчитать по одной из нескольких формул:

где I – сила тока на исследуемом участке эл.цепи; U – напряжение на этом участке; R – сопротивление.

То или иное уравнение для вычислений следует выбирать в зависимости от известных в условии задачи данных.

Закон Джоуля–Ленца

Когда под воздействием эл.поля в цепи не происходит хим.преобразования вещества и не совершается механическая работа, то работа, производимая эл.полем, ведет только к нагреву проводника. Кол-во теплоты, которое при этом выделяет проводник с эл.током, равно:

где t – время, в течение которого совершается работа.

Разбор типовых вариантов заданий №12 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое в цепи за 1 с, может быть получено

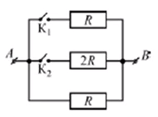
  1. если замкнут только ключ К1
  2. если замкнут только ключ К2
  3. если замкнуты оба ключа
  4. если оба ключа разомкнуты

[/su_note]

Алгоритм решения:

1. Анализируем схему, приведенную в условии. Определяем расчетную формулу.

2–5. Определяем кол-во теплоты в каждой из ситуаций, рассмотренных в утверждениях 1–4. Определяем прав.вариант ответа.

Решение:
  1. По з-ну Джоуля-Ленца 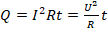. Поскольку имеет место параллельное соединение разных резисторов, то сила тока в каждой ветке будет различаться. А напряжение при этом во всех ветках одинаково. Поэтому в данном случае удобнее воспользоваться 2-й формулой (в которой присутствует напряжение).
  2. Рассм.утверждение 1. Здесь ток будет протекать по двум параллельным веткам – верхней и нижней. Общее сопротивление при этом равно: 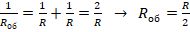. Тогда за 1 с .
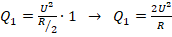  3. В утверждении 2 замкнули ключ 2. Следовательно, ток течет по средней и нижней веткам. В этом случае 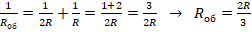. Искомое кол-во теплоты: .
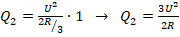  4. Если оба ключа замкнуть, то ток потечет по всем 3 веткам. Отсюда: 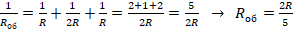. Кол-во теплоты за 1 с в таком случае составит: .
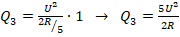  5. В утверждении 4 рассмотрен вариант, когда оба ключа разомкнуты. Это означает, что ток течет только по нижней ветке и .
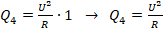  6. Сравним полученные кол-ва теплоты. Сравнивать будем с Q4, поскольку полученная для этой величины формула не содержит коэффициента. Итак: 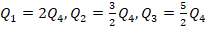. Отсюда видно, что, во-первых, каждое из Q1–Q3 больше, чем Q4, а во-вторых, среди этих трех значений самое большое имеет Q3. Т.е. максимальное кол-во теплоты выделится, если замкнуть оба ключа.

Ответ: 3.

Первый вариант (Камзеева, № 3)

[su_note note_color=»#defae6″]

Из однородной металлической проволоки сделано кольцо. Напряжение на полюсах источника тока постоянно. При каком подключении контакта К потребляемая мощность цепи будет минимальной?

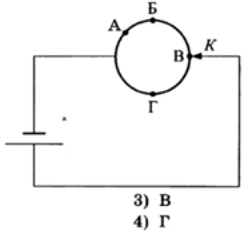
  1. А
  2. Б
  3. В
  4. Г

[/su_note]

Алгоритм решения:
  1. Записываем формулу для расчета мощности через напряжение и сопротивление. Определяем условие, при котором она будет минимальной.
  2. Находим зависимость сопротивления от длин проводников.
  3. Анализируем особенность параллельного соединения проводников и, исходя из этого и выводов п.2, определяем точку подключения ключа.
Решение:
  1. По условию напряжение на источнике тока является постоянной величиной. Поэтому для расчета мощности удобнее всего воспользоваться такой формулой: 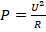. Из этой формулы следует, что минимальная мощность будет в точке, в которой максимально сопротивление.
  2. Сопротивление цилиндрического проводника вычисляется по формуле: 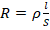. Поскольку проволока однородна, то ρ в данном случае есть величина постоянная. Постоянна и S, т.к. длина кольца не меняется. Поэтому сопротивление здесь пропорционально длине проводника l. Тогда имеем зависимость: чем больше длина проводника, тем больше сопротивление.
  3. Из схемы цепи видно, что в любом случае соединение проводников будет параллельным. А потому тут следует помнить еще один момент: при параллельном соединении проводников общее сопротивление всегда будет меньше самого меньшего из сопротивлений (что можно проверить опытным путем). Самое маленькое сопротивление у проводника А, т.к. у него наименьшая длина (см.п.2). Поэтому в данном случае ключ нужно подключить в точку, которая является самой удаленной от А. Ею является т.В. Именно так получим максимальное сопротивление и, соответственно (см.п.1), минимальную мощность цепи.

Ответ: 3

Второй вариант (Камзеева, № 5)

[su_note note_color=»#defae6″]

На рисунке показано подключение в сеть постоянного напряжения трех одинаковых ламп.

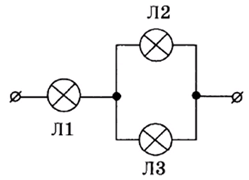
С минимальным накалом будет(-ут) гореть лампа(-ы)

  1. 1
  2. 2
  3. 3
  4. 2 и 3

[/su_note]

Алгоритм решения:
  1. Записываем формулу для расчета эл.мощности ламп через силу тока и сопротивление.
  2. Анализируем приведенную в условии схему и определяем зависимость мощности от силы тока и сопротивления.
  3. Определяем мощность каждой из ламп, сравниваем их.
Решение:
  1. Степень накала ламп зависит от величины тепловой мощности, выделяемой на каждой из них. Для определения электрической мощности используем формулу .
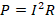  2. Сопротивления у ламп равны между собой, т.к. лампы одинаковы. А сила токов будет различаться на участке Л1 и на участке параллельного соединения ламп Л2 и Л3. При параллельном соединении ток делится, причем, поскольку лампы одинаковы, то ток разделится поровну. Т.е. если принять, что через Л1 идет ток I, то через Л2 и Л3 – токи, равные I/2.
  3. Мощность лампы Л1 будет равной 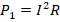, мощности Л2 и Л3 – 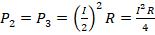. Из этих формул видно, что мощность ламп Л2 и Л3 в 4 раза меньше, чем Л1. Этой ситуации соответствует ответ №4.

Ответ: 4

Третий вариант (Камзеева, № 10)

[su_note note_color=»#defae6″]

Четыре резистора изготовлены из различных материалов и имеют различные размеры (см. рис.).

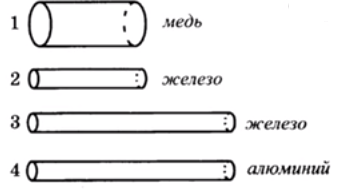
Наибольшее электрическое сопротивление имеет резистор

  1. 1
  2. 2
  3. 3
  4. 4

[/su_note]

Алгоритм решения:
  1. Запишем формулу для вычисления эл.сопротивления цилиндрического проводника.
  2. Находим соотношение длин разных проводников.
  3. Определяем соотношение у разных проводников площадей поперечного сечения.
  4. Определяем соотношения между уд.сопротивлениями.
  5. Находим сопротивление для каждого проводника, сравниваем их величины. Определяем максимальное сопротивление.
Решение:
  1. Поскольку на рисунке изображены цилиндрические проводники, то для определения их сопротивлений можно использовать формулу .
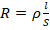  2. Поскольку сопротивление пропорционально длине проводника, то это значит, что чем больше длина, тем больше сопротивление. Этому условию отвечают проводники 3 и 4. Из рисунка видно, что они приблизительно в 2 раза длиннее, чем 1 и 2. Т.е. если принять, что l1=l2=l, то тогда l3=l4=2l.
  3. С площадью все наоборот: чем она больше, тем сопротивление меньше. Поэтому с этой точки зрения менее всего подходит 1-й проводник. У него диаметр (и, соответственно, радиус) примерно в 2 раза больше, чем у остальных; а это означает, что его площадь сечения примерно в 4 раза больше. И если принять, что S2=S3=S4=S, то S1=4S.
  4. 3-й параметр, который тут необходимо участь, – удельное сопротивление (эти значения следует смотреть в соответствующей таблице). Для меди оно равно 0,017 (Ом·мм2/м), для железа – 0,10, для алюминия – 0,028. Соотнесем эти величины с самой маленькой из них – 0,017, обозначив ее ρ. Сравнение дает такие результаты: уд.сопротивление у железа 5,88ρ, а у алюминия – 1,65ρ.
  5. Делаем общий вывод. Для 1-го проводника 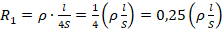. Для 2-го проводника 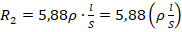. Для 3-го проводника 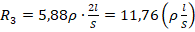. Для 4-го проводника 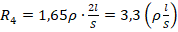. Отсюда видно, что максимальное сопротивление имеет проводник 3.

Ответ: 3

Текст: Базанов Даниил, 12.7k 👀