Задание №16 ОГЭ по физике

Электродинамика: расчетная задача

Для успешного решения задания №16 ОГЭ по физике необходимо знание всего раздела электродинамики, начиная от понятия эл.заряда и электризации физ.тел и заканчивая расчетными формулами для определения работы и мощности. Часть теоретических сведений приведена в разделе теории к этому заданию. Остальную нужную информацию рекомендуется искать в разделах теории к заданиям №№11,12, имеющих содержание, в той или иной степени подобное заданию №16.

Теория к заданию №16 ОГЭ по физике

Работа и мощность

Видов работы в физике существует несколько, в частности, говоря о работе механической, термодинамической, сил эл.поля. Механическую работу совершают силы, приложенные к объектам макромира (в общем случае – к материальной точке), термодинамическая подразумевает изменение внутр.энергии физ.тела. Работа сил эл.тока заключается в перемещении заряда из одной его точки в другую, отличную от первоначальной.

В общем случае работа может быть определена так:

A=N·t

где N – мощность, t – время совершения работы.

Из этой формулы логично следует определение понятия мощности. Мощность – это работа, выполняемая за единицу времени, т.е. скорость выполнения работы. А поскольку работа в физике заключается в преобразования (потреблении, передаче) энергии, то мощность характеризуют как скорость такого преобразования (потребления, передачи).

В зависимости от того, какие именно силы совершают работу, она вычисляется по той или иной формуле. Поскольку тематика данного задания – электродинамические силы, то для расчетов следует использовать уравнения:

где I – сила тока в эл.цепи, в которой совершается работа; U – напряжение, R – сопротивление.

Соответственно, мощность в этом случае должна определяться как:

КПД

КПД – коэффициент полезного действия – показатель эффективности системы, осуществляющей преобразование и (или) передачу энергии. Системой в данном случае может выступать устройство, механизм и т.п. КПД в физике принято обозначать греческой буквой ɳ («эта»).

Вычисляется КПД по формулам:

где Еп, Ап, Nп – соответственно полезная энергия, работа, мощность; Е, А, N – полная (затраченная) энергия, работа, мощность.

Часто при решении задач оперируют с КПД, выраженным не в процентах, а в долях. Так бывает удобнее при выполнении математических вычислений. В этом случае в формуле для КПД исчезает множитель 100, и она приобретает вид:

Разбор типовых вариантов заданий №16 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

Электродвигатель работает при напряжении 220 В и силе тока 40 А. Чему равна полезная мощность двигателя, если известно, что его КПД составляет 75 %?

[/su_note]

Алгоритм решения:
  1. Переводим КПД из процентов в доли для упрощения вычислений.
  2. Записываем формулу для вычисления КПД через работу (1).
  3. Записываем уравнение для расчета полезной мощности (2).
  4. Подставляем (2) в (1), получаем формулу (3). Выражаем затраченную работу через величины U и I, данные в условии. Получаем (4).
  5. Формулу (4) подставляем в (3). Из полученного уравнения выражаем искомую мощность. Вычисляем ее.
Решение:
  1. ɳ=75 %=0,75.
  2. КПД двигателя в данном случае следует рассчитывать по формуле: .
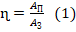  3. Поскольку двигатель совершает механическую работу, то его полезная мощность равна: 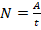, где А – полезная работа, т.е. А=АП. Отсюда АП=N·t (2).
  4. (2) → (1): 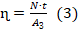. Поскольку по условию работает электродвигатель, то затраченная работа в данном случае может быть определена по одной из формул для работы, использующихся в электродинамике. Поскольку в условии даны напряжение и сила тока, то оптимальной является формула: AЗ=IU·t (4).
  5. (4) → (3): 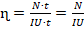. Выразим отсюда искомую мощность: N=ɳIU. Вычислим мощность: N=0,75·40·220=6600 (Вт). Т.к в ответе требуется записать ответ в кВТ, то получаем: 6600 Вт=6,6·103 Вт=6,6 кВт.

Ответ: 6,6

Первый вариант (Камзеева, № 4)

[su_note note_color=»#defae6″]

Три лампы, каждая сопротивлением 240 Ом, соединены последовательно и включены в сеть, напряжение которой 120 В. Определите мощность, потребляемую всеми лампами.

[/su_note]

Алгоритм решения:
  1. Записываем соответствующую формулу для вычисления мощности (1).
  2. Находим общее сопротивление в сети (2).
  3. Подставляем (2) в (1), получаем формулу для определения искомой мощности. Находим ее.
Решение:
  1. Поскольку в условии задачи даны напряжение в сети и сопротивление ламп, то для расчета мощности используем формулу 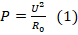, где R0 – общее сопротивление в сети.
  2. Т.к. лампы в сети соединены последовательно, то R0=R+R+R=3R (2), где R – сопротивление каждой лампы.
  3. (2) → (1): 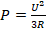. Найдем мощность: .

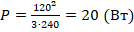Ответ: 20

Второй вариант (Камзеева, № 7)

[su_note note_color=»#defae6″]

Исследуя зависимость силы тока от напряжения на резисторе при его постоянном сопротивлении, ученик получил результаты, представленные в таблице. Чему равно удельное сопротивление металла, из которого изготовлен резистор, если длина провода 5 м, а площадь его поперечного сечения 1 мм2?

[/su_note]

Алгоритм решения:
  1. Записываем формулу для вычисления сопротивления из з-на Ома для участка цепи (1).
  2. Записываем уравнение для сопротивления через уд.сопротивление (2).
  3. Приравниваем (1) и (2). Выражаем из полученного уравнения уд.сопротивление.
  4. Определяем из таблицы числовые данные, необходимые для расчета искомой величины.
  5. Вычисляем уд.сопротивление.
Решение:
  1. По з-ну Ома для участка цепи 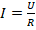. Отсюда: .
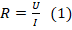  2. С другой стороны сопротивление .
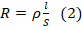  3. (2=3): .
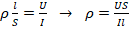  4. Из таблицы возьмем произвольно пару соответствующих друг другу значений для U и I. Самыми простыми для расчетов здесь являются значения U=1 B, I=2 A. Площадь попер.сечения, выраженную в условии в мм2, переводить в СИ не будем, поскольку в задаче требуется дать ответ в [Ом·мм2/м].
  5. Найдем уд.сопротивление: .

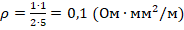Ответ: 0,1

Третий вариант (Камзеева, № 10)

[su_note note_color=»#defae6″]

Определите показания амперметра, если показания вольтметра равны 12 В.

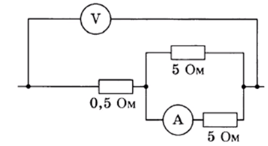
[/su_note]

Алгоритм решения:
  1. Записываем формулу для вычисления силы тока в цепи.
  2. Находим сопротивление на отдельных частях заданного участка цепи и общее сопротивление.
  3. Находим силу тока в цепи, а затем, зная ее, определяем показания амперметра.
Решение:
  1. Если известны сопротивления всех резисторов и напряжение в сети, то можно определить и силу тока в цепи. Для этого подходит з-н Ома для участка цепи: 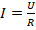. Здесь R – общее сопротивление на участке, охваченном вольтметром (далее обозначим его как Rобщ).
  2. Из схемы видно, что участок цепи состоит из двух последовательно соединенных частей – резистора с сопротивлением в 0,5 Ом и параллельной ветки с резисторами по 5 Ом. Поэтому Rобщ=R´+R´´, где R´ – сопротивление на участке до ветвления, R´´ – сопротивление в параллельной ветке (обозначим их как R1). Тогда получим, что R´=0,5 (Ом). Для R´´ произведем расчет: 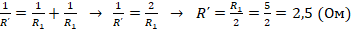. Отсюда: Rобщ=0,5+2,5=3 (Ом).
  3. Найдем силу тока в сети: 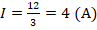. С такой силой ток проходит через 1-й резистор (в 0,5 Ом). В параллельной ветке сила тока делится, причем в данном случае делится пополам, поскольку резисторы одинаковы. Отсюда следует, что показания амперметра будут таковы: .

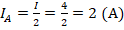Ответ: 2

Текст: Базанов Даниил, 2.5k 👀