Элементы теории чисел
19 задание в профильном уровне ЕГЭ по математике направлено на выявление у учеников способности оперировать числами, а именно их свойствами. Это задание наиболее сложное и требует нестандартного подхода и хорошего знания свойств чисел. Перейдем к рассмотрению типового задания.
Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=»#defae6″]
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
[/su_note]
Алгоритм решения:
- Вводим переменные k, l, m.
- Находим сумму набора чисел.
- Отвечаем на пункт а).
- Определяем, каких чисел больше (пункт б)).
- Определяем, сколько положительных чисел.
Решение:
1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.
2. Сумма выписанных чисел равна их количеству в данной записи на доске, умноженному на среднее арифметическое. Определяем сумму:
4k −8l + 0⋅m = − 3(k + l +m)
3. Заметим, что слева в приведенном только что равенстве каждое из слагаемых делится на 4, потому сумма количества каждого типа чисел k + l + m тоже делится на 4. По условию общее число записанных чисел удовлетворяет неравенству:
40 < k + l + m < 48
Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4.
Значит, написано на доске всего 44 числа.
4. Определяем, чисел какого вида больше: положительных или отрицательных. Для этого приведем равенство 4k −8l = − 3(k + l +m) к более упрощенному виду: 5l = 7k + 3m.
5. m≥ 0. Отсюда вытекает: 5l ≥ 7k, l > k. Получается, что отрицательных чисел записано больше положительных. Подставляем вместо k + l + m число 44 в равенство
4k −8l = − 3(k + l + m).
Имеем
4k − 8l = −132, k = 2l − 33
k + l ≤ 44, тогда получается: 3l − 33 ≤ 44; 3l ≤ 77; l ≤ 25; k = 2l − 33 ≤17. Отсюда приходим к выводу, что положительных чисел не более 17.
Если же положительных чисел всего 17, то на доске 17 раз записано число 4, 25 раз – число −8 и 2 раза записано число 0. Такой набор отвечает всем требованиям задачи.
Ответ: а) 44; б) отрицательных; в) 17.
Второй вариант 1 (из Ященко, №1)
[su_note note_color=»#defae6″]
На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.
а) Может ли на доске быть ровно 27 чётных чисел?
б) Могут ли ровно два числа на доске оканчиваться на 3?
в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?
[/su_note]
Алгоритм решения:
- Приведем пример набора чисел, который удовлетворяет условию (Это подтверждает возможность набора чисел).
- Проверяем вероятность второго условия.
- Ищем ответ на третий вопрос, введя переменную n.
- Записываем ответы.
Решение:
1. Такой примерный перечень чисел на доске соответствует заданным условиям:
3,13,23,33,43,53,63,73,2,4,6,…,50,52,56
Это дает положительный ответ на вопрос а.
2. Пусть на доске написано ровно два числа, у которых последняя цифра 3. Тогда там записано 33 чётных числа. Их сумма:
![]()
Это противоречит тому, что сумма написанных чисел равна 1062, то есть, утвердительного ответа на вопрос б нет.
3. Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n)из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна
![]()
а сумма чётных:
2+4+…+2(35 – n)=(35 – n)(36 – n)= n2-71 n+1260.
Тогда из условия:
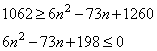
Решаем получившееся неравенство:
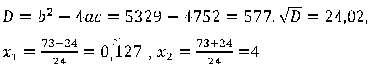
Получается, что ![]() . Отсюда, зная, что n — натуральное, получаем
. Отсюда, зная, что n — натуральное, получаем ![]() .
.
3. Наименьшее число чисел, оканчивающихся на 3, может быть только 5. И добавлено 30 чётных чисел, тогда сумма всех чисел нечётна. Значит, чисел, которые оканчиваются на 3, больше. чем пять, поскольку сумма по условию равна четному числу. Попробуем взять 6 чисел, с последней цифрой 3.
Приведём пример, когда 6 чисел, оканчиваются на три, и 29 чётных чисел. Сумма их равна 1062. Получается такой список:
3, 13, 23, 33, 43, 53, 2, 4, …, 54, 56, 82.
Ответ: а) да; б) нет; в) 6.
Третий вариант (из Ященко, №4)
[su_note note_color=»#defae6″]
Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 17 дней?
б) Могли ли они фотографировать в течение 18 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?
[/su_note]
Алгоритм решения:
- Ответим на вопрос а).
- Найдем ответ на вопрос б).
- Найдем суммарное количество фотографий, сделанных Наташей.
- Запишем ответ.
Решение:
1. Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала ![]() снимков.
снимков.
Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала
![]() кадров.
кадров.
Найдем такие m и n, чтобы выполнялось равенство:
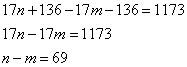
Возьмем, к примеру, n=70 и m=1. Это ответ на вопрос а).
2. Если фотографировали девочки всего 18 дней, получается:
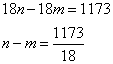
1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя. Это ответ на вопрос б.
3. Поищем ответ на последний вопрос. Допускаем, что девочки делали фотографии x дней. Тогда Маша сделала бы в последний день снимков
![]()
То есть ![]() . А согласно условию
. А согласно условию
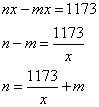
число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3.
Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:
Для числа x=3:
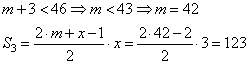
При x=17:
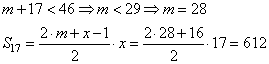
А при x=23:
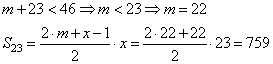
Самое большое количество снимков, которые сделала Наташа:
759+1173=1932.
Ответ: а) да; б) нет; в) 1932.