Задание №20 ЕГЭ по математике базового уровня

Задачи на сообразительность

Задание №20 ЕГЭ по математике содержит задачу на сообразительность. Задачи в этом разделе более интуитивно понятно, нежели в 19 задании ЕГЭ, но тем не менее достаточно сложны для обычного школьника. Итак, перейдем к рассмотрению типовых вариантов.

Разбор типовых вариантов заданий №20 ЕГЭ по математике базового уровня

Вариант 20МБ1

[su_note note_color=»#defae6″]

В обменном пункте можно совершить одну из двух операций:

  • за 2 золотых монеты получить 3 серебряных и одну медную;
  • за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

[/su_note]

Алгоритм выполнения:
  1. Ввести условные обозначения.
  2. Записать данные задачи с помощью условных обозначений.
  3. Логически рассуждая определить неизвестное.
Решение:

По условию золотых монет не появилось, значит все полученные после осуществления второй операции золотые монеты, Николай обменял с помощью первой операции. Золотые монеты можно менять только по 2 штуки, следовательно, вторых операций было четное число.

Введем обозначение, пусть вторых операций было 2n(число всегда четное).

Если применить вторую операцию получим:

5 · 2n серебряных обменяли на 3 · 2n золотых + 2n медных.

Все золотые монеты были обменяны в ходе первой операции. За одну операцию можно обменять сразу 2 золотые монеты, значит, всего операций будет совершено (3 · 2n)/2 = 3 n. То есть

3 · 2n золотых обменяли на 3· 3n серебряных + 3n медных.

Или после преобразования:

3 · 2n золотых обменяли на 9n серебряных + 3n медных

Сопоставим результаты первой и второй операции:

5 · 2n серебряных обменяли на 3 · 2n золотых + 2n медных.

3 · 2n золотых обменяли на 9n серебряных + 3n медных

Получим

5 · 2n серебряных обменяли на 9n серебряных + 3n медных+2n медных

Или

10 n серебряных обменяли на 9n серебряных + 5n медных

Если, обменяв 10 n серебряных монет, получим 9 n серебряных монет, то количество серебряных монет у Николая уменьшилось на n. Из последнего выражения видно, что Николай получил 5n медных монет, а по условию появилось 50 медных, то есть 5n = 50.

n = 10

Ответ: 10

Вариант 20МБ2

[su_note note_color=»#defae6″]

Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

[/su_note]

Алгоритм выполнения:
  1. Определить, кто и во сколько раз дольше ел печенье.
  2. Определить, кто и во сколько раз дольше ел варенье.
  3. Сопоставить результаты.
  4. Найти неизвестное.
Решение:
  1. Так как варенье и Маша, и Медведь съели поровну, и при этом Медведь ел варенье в 3 раза быстрее, то Маша ела варенье (свою половину) в 3 раза дольше, чем Медведь (такую же половину).
  2. Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем.
  3. В сумме эти печенья составляют 1+9=10 и таких сумм в 100 печеньях ровно 100:10 = 10.
  4. Значит, Маша съела 10 печений, а Медведь 9∙10=90.

Ответ: 90

Вариант 20МБ3

[su_note note_color=»#defae6″]

Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

[/su_note]

Алгоритм выполнения:
  1. Определить, кто и во сколько раз дольше ел печенье.
  2. Определить, кто и во сколько раз дольше ел варенье.
  3. Сопоставить результаты.
  4. Найти неизвестное.
Решение:
  1. Так как варенье и Маша, и Медведь, съели поровну, и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину).
  2. Тогда получается, что Медведь ел печенья в 4 раза дольше Маши и к тому же ел их в 4 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 4∙4=16 печений, съеденных Медведем.
  3. В сумме эти печенья составляют 1+16=17 и таких сумм в 51 печеньях ровно 51:17 = 3.
  4. Значит, Маша съела 3 печенья, а Медведь 3∙16=48.

Ответ: 48

Вариант 20МБ4

[su_note note_color=»#defae6″]

Если бы каждый из двух сомножителей увеличили на 1, их произведение увеличилось бы на 11. На самом деле каждый из двух сомножителей увеличили на 2. На сколько увеличилось произведение?

[/su_note]

Алгоритм выполнения:
  1. Ввести условные обозначения.
  2. Записать первое условие с помощью условных обозначений.
  3. Преобразовать полученное выражение.
  4. Записать с помощью условных обозначений второе условие.
  5. Преобразовать полученное выражение.
  6. Найти неизвестное.
Решение:

Пусть первый сомножитель равен a, а второй b, их произведение равно ab.

При увеличении этих сомножителей на 1 их произведение возрастает на 11, то есть,

image001Перенесем произведение ab в левую часть с противоположным знаком и раскроем скобки перемножив.

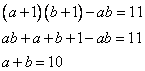
image002

Теперь аналогично вычислим, на сколько увеличится произведение, если сомножители увеличить на 2 и подставим уже известное нам a + b = 10 :

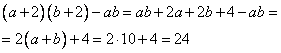
image003

Ответ: 24

Вариант 20МБ5

[su_note note_color=»#defae6″]

Если бы каждый из двух сомножителей увеличили на 1, их произведение увеличилось бы на 3. На самом деле каждый из двух сомножителей увеличили на 5. На сколько увеличилось произведение?

[/su_note]

Алгоритм выполнения:
  1. Ввести условные обозначения.
  2. Записать первое условие с помощью условных обозначений.
  3. Преобразовать полученное выражение.
  4. Записать с помощью условных обозначений второе условие.
  5. Преобразовать полученное выражение.
  6. Найти неизвестное.
Решение:

Пусть первый сомножитель равен a, а второй b, их произведение равно ab.

При увеличении этих сомножителей на 1 их произведение возрастает на 3, то есть,

image001

Перенесем произведение ab в левую часть с противоположным знаком и раскроем скобки перемножив.

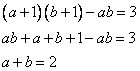
image002

Теперь аналогично вычислим, на сколько увеличится произведение, если сомножители увеличить на 5 и подставим уже известное нам a + b = 2:

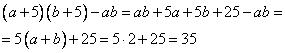
image003

Ответ: 35

Вариант 20МБ6

[su_note note_color=»#defae6″]

Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными отрезками. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

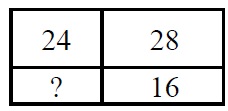
ЕГЭ по математике задание №20

[/su_note]

Перерисуем прямоугольник в удобном для нас виде:

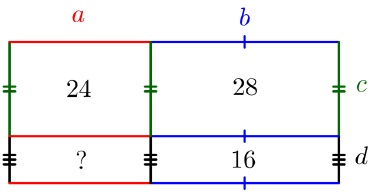
ЕГЭ по математике задание №20

Теперь составим уравнения с помощью формулы периметра прямоугольника:

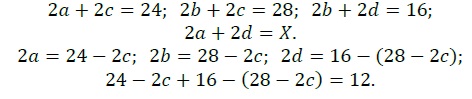
ЕГЭ по математике задание №20

Ответ: 12

Вариант 20МБ7

[su_note note_color=»#defae6″]

Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?

[/su_note]

Алгоритм выполнения
  1. Составляем комбинации правильных и неправильных ответов и определяем кол-во баллов в них, например: 1) 1 прав+1 неправ=7–10=–3 балла; 2) 2 прав+1неправ=2·7–10=4 балла и т.д.
  2. Из баллов за прав.ответы и баллов за их комбинации «набираем» 42 балла. Подсчитываем кол-во вопросов, которые при этом были заданы.
  3. Оставшуюся разницу между полученным числом вопросов и данными 25-ю вопросами определяем как те, на которые не было дано ответа.
  4. Делаем проверку полученного результата.
Решение:

Введем обозначения: прав.ответ – 1П, неправ.ответ – 1Н.

Задаем комбинации и определяем кол-во баллов, которое при этом будет начислено:

1П=7 баллов

1П+1Н=7–10=–3 б.

2П+1Н=2·7–10=4 б.

3П+1Н=3·7–10=11 б.

Суммируем баллы, которые можно при этом получить: 7+ (–3)+4+11=19. Это явно мало. И гарантированно можно добавить еще 11: 19+11=30. Чтобы «добрать» до 42 баллов, нужно далее добавить 12 баллов, которые набираются тройным вхождением 4-х баллов. В целом получаем:

7+(–3)+4+11+11+3·4=42.

Распишем полученную комбинацию слагаемых в виде ответов:

1П+(1П+1Н)+(2П+1Н)+(3П+1Н)+(3П+1Н)+3·(2П+1Н)=1П+1П+1Н+2П+1Н+3П+1Н+3П+1Н+6П+3Н=16П+7Н (ответов).

16+7=23 ответа. 25–23=2 ответа, за которые было получено по 0 баллов, т.е. это вопросы, оставшиеся без ответов.

Итак, по нашим подсчетам верных ответов было дано 16.

Проверим это:

16 ответов по 7 б. + 7 ответов по (–10) б. + 2 ответа по 0 б. = 16·7–7·10+2·0=112–70+0=42 (балла).

Ответ: 16

Вариант 20МБ8

[su_note note_color=»#defae6″]

В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором – 97, в третьем – 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?

[/su_note]

Алгоритм выполнения
  1. Находим общую сумму для всех чисел в таблице (сложив суммы для каждого из 3-х столбцов).
  2. Определяем диапазон допустимых значений для сумм чисел в каждой строке.
  3. Разделив общую сумму сначала на наименьшую сумму чисел в каждой строке, а затем на наибольшую, получаем искомое кол-во строк.
Решение:

Общая сумма чисел в таблице равна: 103+97+93=293.

Поскольку по условию суммы чисел в каждой строке составляют >21, но <24, то кол-во строк X может быть равным меньше, чем 293:21≈13,95, и больше, чем 293:24≈12,21. Т.е.: 12,21 < X < 13,95. Единственное целое число в полученном диапазоне – 13. Значит, искомое кол-во строк равно 13.

Ответ: 13

Вариант 20МБ9

[su_note note_color=»#defae6″]

В доме всего восемнадцать квартир с номерами от 1 до 18. В каждой квартире живет не менее одного и не более трех человек. В квартирах с 1-й по 13-ю включительно живет суммарно 15 человек, а в квартирах с 11-й по 18-ю включительно живет суммарно 20 человек. Сколько всего человек живет в этом доме?

[/su_note]

Алгоритм выполнения
  1. Определяем максимальное кол-во живущих в 11–13-й квартирах, используя данные о том, сколько человек живет в 1–13-й квартирах.
  2. Находим минимальное число жильцов 11–13-й квартир, учитывая данные о живущих в 11–18-й квартирах.
  3. Сопоставляет данные, полученные в пп.1–2, получаем точное кол-во жильцов этих квартир №№11–13.
  4. Находим кол-во живущих в квартирах 1–10-й и 14–18-й.
  5. Вычисляем общее число жильцов дома.
Решение:

В первых 13 квартирах (с 1-й по 13-ю) живет 15 человек. Это означает, что в 11-ти квартирах живет по 1 человеку плюс в 2-х квартирах по 2 человека (11·1+2·2=15). Следовательно, в 11–13-й (т.е. в 3-х) квартирах проживает не менее 3-х и не более 5 (1+2+2) человек.

Во вторых 8 квартирах (11-й по 18-ю) проживает 20 человек. При этом с 14-й по 18-ю квартиры (т.е. в 5 квартирах) не может проживать более чем 5·3=15 человек. А следовательно, в 11-13-й квартирах живет не менее, чем 20–15=5 человек.

Т.е. с одной стороны в 11-13-й квартирах должно жить не более 5 человек, а с другой – не менее 5. Вывод: в этих квартирах живет ровно 5 человек, т.к. других допустимых для обоих случаев значений тут нет.

Тогда получаем: в 1–10-й квартирах живет 15–5=10 человек, в 14–18-й – 20–5=15 человек. Всего в доме проживает: 10+5+15=30 человек.

Ответ: 30

Вариант 20МБ10

[su_note note_color=»#defae6″]

В обменном пункте можно совершить одну из двух операций:

  • за 4 золотых монеты получить 5 серебряных и одну медную;
  • за 7 серебряных монет получить 5 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?

[/su_note]

Алгоритм выполнения
  1. Определяем кол-во серебряных монет, которые необходимы Николаю для совершения двойного обмена так, чтобы у него не появились золотые монеты. Двойной обмен – это обмен сначала серебряных монет на золотые и медные, а затем золотые на серебряные и медные.
  2. Определяем кол-во разных монет, которые появятся у Николая в результате 1 двойного обмена.
  3. Вычисляем кол-во двойных обменов, которые необходимо совершить, чтобы появилось 45 медных монет.
  4. Находим кол-во серебряных монет, которые должен был иметь Николай изначально, чтобы совершить нужное кол-во обменов, и которые получил в результате всех обменов.
  5. Определяем искомую разницу.
Решение:

Совершить 1-й обмен Николай должен по 2-й схеме, т.к. у него есть только серебряные монеты. Для того же, чтобы в результате у него не оказалось золотых монет, нужно найти минимальное кратное для 5 золотых, которые он получит, и 4 золотых, которые у него за 1 раз могут принять в полном объеме (без остатка). Это – число 20.

Соответственно, чтобы получить 20 золотых монет, у Николая должно быть 20:5=4 комплекта серебряных монет по 7 штук. Значит, первоначально их у него должно быть 4·7=28. И при этом Николай получает еще и 1·4=4 медных монеты.

Совершая обмен, Николай отдает 20:4=5 комплектов золотых медалей. Взамен он получает 5·5=25 серебряных монет и 1·5=5 медных монет.

Т.о., в результате одного обмена у Николая появится 25 серебряных монет и 4+5=9 медных монет. Поскольку в итоге у Николая оказалось 45 медных монет, значит, было совершено 45:9=5 двойных обменов.

Если в результате 1 двойного обмена у Николая оказалось 25 серебряных монет, то после 5 таких обменов у него их окажется 25·5=125 штук. А первоначально он должен был для этого иметь 28·5=140 серебряных монет. Следовательно, их количество у Николая уменьшилось на 140–125=15 штук.

Ответ: 15

Вариант 20МБ11

[su_note note_color=»#defae6″]

Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нем 357 квартир?

[/su_note]

Алгоритм выполнения
  1. Определяем уравнение для определения кол-ва квартир в доме всего через параметры, заявленные в условии (т.е. через кол-во квартир на этаже и т.д.).
  2. Раскладываем 357 на множители.
  3. Находим соответствие полученных множителей конкретным параметрам, сходя из условия о том, какой из параметров больше или меньше прочих.
Решение:

Т.к. на всех этажах одинаковое кол-во квартир (Х), по всех подъездах одинаковое кол-во этажей (Y), то обозначив кол-во подъездов через Z, можем записать: 357=X·Y·Z.

Разложим 357 на простые множители. Получим: 357=3·7·17·1. Причем это единственный вариант расклада. Т.к. Y>X>Z>1, то единицу в раскладе не учитываем и определяем, что Z=3, X=7, Y=17.

Поскольку кол-во этажей было обозначено через Y, то искомое число – 17.

Ответ: 17

Вариант 20МБ12

[su_note note_color=»#defae6″]

Из десяти стран семь подписали договор о дружбе ровно с тремя странами, а каждая из оставшихся трех – ровно с семью. Сколько всего было подписано договоров?

[/su_note]

Алгоритм выполнения
  1. Подсчитываем кол-во договоров, подписанных 7-ю странами.
  2. Определяем кол-во договоров, которые подписали 3 оставшиеся страны.
  3. Находим общее кол-во подписанных договоров. Делим его на 2, т.к. договоры двусторонние.
Решение:

Первые 7 стран подписали договоры с 3 странами, т.е. на этих договорах поставлено 7·3=21 подпись. Аналогично остальные 3 страны при оформлении договоров с 7-ю странами поставили 3·7=21 подпись. Значит, всего поставлено 21+21=42 подписи.

Т.к. все договоры двусторонние, то это значит, что на каждом из них зафиксировано 2 подписи. Следовательно, договоров вдвое меньше, чем подписей, т.е. 42:2=21 договор.

Ответ: 21

Вариант 20МБ13

[su_note note_color=»#defae6″]

На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведенные линии разделили поверхность глобуса?

Меридиан – это дуга окружности, соединяющая Северный и Южный полюсы. Параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора.

[/su_note]

Алгоритм выполнения
  1. Доказываем, что параллели делят глобус на 13+1 часть.
  2. Доказываем, что меридианы делят глобус на 25 частей.
  3. Определяем кол-во частей, на которые в целом разделен глобус, как произведение найденных чисел.
Решение:

Если всякая параллель – это окружность, то она является замкнутой линией. А это означает, что 1-я параллель делит глобус на 2 части. Далее 2-я параллель обеспечивает деление на 3 части, 3-я – на 4 и т.д. В итоге 13 параллелей разделят глобус на 13+1=14 частей.

Меридиан является дугой окружности, соединяющей полюса, т.е. замкнутой линией она не является и глобус на части не делит. А вот 2 меридиана уже делят, т.е. 2 меридиана обеспечивают деление на 2 части, далее 3-й меридиан добавляет 3-ю часть, 4-й – 5-ю часть и т.д. Значит, в конечном счете, 25 меридианов создает на глобусе 25 частей.

Всего частей на глобусе получается: 14·25=350 частей.

Ответ: 350

Вариант 20МБ14

[su_note note_color=»#defae6″]

В корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков в корзине?

[/su_note]

Алгоритм выполнения
  1. Определяем кол-во груздей среди 12 грибов и рыжиков среди 20 грибов.
  2. Доказываем, что имеется единственно верное число, отображающее кол-во рыжиков. Фиксируем его в ответе.
Решение:

Если среди 12 грибов есть как минимум 1 рыжик, значит, груздей здесь не более 11. Если среди 20 грибов имеется не менее 1 груздя, то тут не более 19 рыжиков.

Это означает, что если груздей не может быть больше 11, то рыжиков не может быть меньше 30–11=19 штук. Т.е. рыжиков с одной стороны не больше 19, а с другой – не меньше 19. Следовательно, рыжиков может быть только ровно 19.

Ответ: 19

Вариант 20МБ15

[su_note note_color=»#defae6″]

Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 3. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 5?

[/su_note]

Алгоритм выполнения
  1. Вводим обозначения для множителей. Это позволит выразить и первоначальное произведение (до увеличения множителей).
  2. Составляем уравнение для ситуации, когда множители увеличены на 1. Выполняем преобразования. Получаем новое выражение, отображающее связь между первоначальными множителями.
  3. Составляем уравнение для ситуации, когда множители увеличены на 5. Выполняем преобразования. Вводим в уравнение выражение, полученное в п.2, находим искомую разницу.
Решение:

Пусть 1-й множитель равен х, 2-й – у. Тогда их произведение – ху.

После того, как множители увеличены на 1, получаем:

(х+1)(у+1)=ху+3

ху+у+х+1=ху+3

х+у=2

После увеличения множителей на 5 имеем:

(х+5)(у+5)=ху+N, где N – искомая разница произведений.

Выполняем преобразования:

ху+5у+5х+25=ху+N

N=ху+5у+5х+25– ху

N=5(х+у)+25

Т.к. выше уже определено, что х+у=2, то получим:

N=5·2+25=35.

Ответ: 35

Вариант 20МБ16

[su_note note_color=»#defae6″]

Саша пригласил Петю в гости, сказав, что живет в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живет Саша? (На всех этажах число квартир одинакова, нумерация квартир в доме начинается с единицы.)

[/su_note]

Алгоритм выполнения
  1. Способом подбора определяем кол-во квартир на площадке. Это должно быть такое число, чтобы номер квартиры оказался большим, чем кол-во квартир в 6-ти подъездах, однако меньшим, чем кол-во квартир в 7-ми.
  2. Определяем кол-во квартир в 6-ти подъездах. От 462 отнимаем это кол-во и делим на число квартир на площадке. Так узнаем искомый номер этажа. Примечание: 1) если получено целое число, то искомый номер этажа на 1 больше, чем вычисленное значение; 2) если получено дробное число, то номером этажа будет округленный в большую сторону результат.
Решение:

Ищем кол-во квартир на площадке, проверяя число за числом.

Предположим, что это кол-во равно 3. Тогда получим, что в 7 подъездах на 6 этажах имеется 7·6·3=126 квартир,

а в 7 подъездах на 7 этажах 7·7·3=147 квартир.

Квартира №462 точно не попадает в диапазон квартир №№126–147.

Аналогично проверяя числа 4, 5 и т.д., придем к числу 10. Докажем, что именно оно подходит:

в 7 подъездах на 6 этажах находится 7·6·10=420 квартир,

в 7 подъездах на 7 этажах: 7·7·10=490 квартир. Поскольку 420<462<490, то условие задания выполнено.

Для того чтобы попасть в квартиру №462, нужно пройти мимо 462–420=42 квартир. Т.к. на каждой площадке находится 10 квартир, то 42:10=4,2 этажей для этого нужно преодолеть. 4,2 означает, что 4 этажа нужно пройти полностью и подняться на 5-й. Т.о., искомый этаж – 5-й.

Ответ: 5

Текст: Базанов Даниил, 16.7k 👀