Задание №25 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Чтобы решить задание № 25, необходимо знание процессов, связанных с понятием механических энергий – кинетической и потенциальной, – а также их взаимных преобразований. В задачах рассматривается движение тел под воздействием различных сил, поэтому требуется понимание того, что представляет собой компенсация одной силы другой (или другими) и равнодействующая сил. Центральными понятиями при этом являются законы сохранения, изучаемые в курсе механики.
Задание ЕГЭ-Ф-ДВ2023-25
Алгоритм решения:
Решение:
Запишем исходные данные:
В СИ нужно перевести только площадь:
S = 2500 см2 = 2500/10 000 м3 = 0,25 м3
Сделаем рисунок и обозначим на нем силы, которые действуют на льдину:
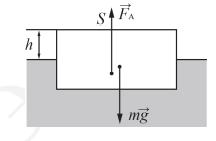
Льдина плавает на поверхности воды, некоторая ее часть выступает над ней. Она не тонет и не всплывает. Следовательно, все приложенные к ней силы уравновешены. В частности, на нее действуют 2 силы:
Так как силы уравновешены и направлены вдоль одной прямой, их проекции равны:
![]()
Или:
![]()
Или:
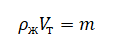
m — масса льдины, ρж — плотность жидкости, в которую погружена льдина (то есть, воды). Vт — объем той части льдины, которая погружена в воду. Его можно вычислить по формуле:
![]()
За H мы обозначили полную высоту льдины.
Следовательно:
![]()
Мы также можем считать, что масса льдины равна:
![]()
V — полный объем льдины, ρ — ее плотность.
Приравняем правые части уравнений:
![]()
Или:
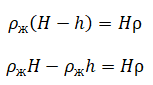
Найдем высоту льдины:
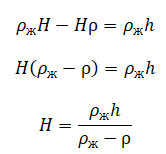
Отсюда масса льдины равна:
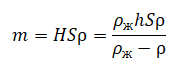
Подставим известные данные и вычислим массу льдины:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22473
На высоте 200 км давление воздуха составляет примерно 10–9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Ответ:
а) 8,31⋅ 10–11 кг/м3
б) 1,38⋅ 10–9 кг/м3
в) 3⋅ 10–10 кг/м3
г)29⋅ 10–8 кг/м3
Алгоритм решения
Решение
Запишем исходные данные:
Запишем уравнение Менделеева — Клапейрона:
pV=mMRT
Плотность определяется формулой:
ρ=mV
Следовательно, масса равна произведению плотности на объем. Перепишем уравнение состояния идеального газа, учитывая, что объем сократится слева и справа:
p=ρMRT
Молярная масса воздуха — табличная величина, равная 28,97 г/моль. Переведем в СИ и получим 28,97∙10–3 кг/моль.
Выразим и вычислим плотность:
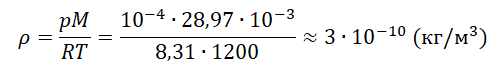
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22795
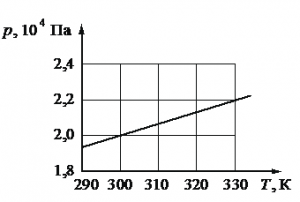 На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
Алгоритм решения
Решение
Запишем исходные данные. Объем сосуда равен: V = 0,25 м3. На графике выберем точку, соответствующую температуре T = 300 К. Ей соответствует давление p = 2∙104 Па.
Запишем уравнение состояния идеального газа:
pV=νRT
Отсюда количества вещества равно:
ν=pVRT=2·104·0,258,31·300≈2 (моль)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17615
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 2 раза. Какова первоначальная абсолютная температура газа?
Ответ:
а) 600 К
б) 400 К
в) 350 К
г) 300 К
Алгоритм решения
Решение
Запишем исходные данные:
По условию задачи это изохорный процесс, следовательно он происходит в соответствии с законом Шарля:
p1T1=p2T2
Выразим конечную температуру и получим:
T2 = T1 – ∆T
Перепишем закон Шарля применительно к задаче и выразим первоначальную температуру:
2pT1=pT1−ΔT
2(T1−ΔT)=T1
2T1−T1=2ΔT
T1=2ΔT=2·200=400 (К)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
Решение
Запишем исходные данные:
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
Отсюда:
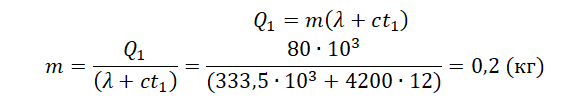
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
![]()
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22543
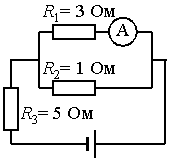 В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
Ответ:
а) 23 В
б) 25 В
в) 27 В
г) 29 В
Алгоритм решения
Решение
Запишем исходные данные:
Закон Ома для полной цепи:
I=εR+r
R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:
1R12=1R1+1R2
R12=R1R2R1+R2
Полное сопротивление внешней цепи равно:
R=R12+R3=R1R2R1+R2+R3
Следовательно, ЭДС источника тока равен:
ε=I(R+r)=I(R1R2R1+R2+R3+r)
Полная сила тока равна силе тока параллельного участка цепи, так как I = I3 = I12. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:
I12=I1+I2=I
Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:
U1=I1R1
Так как это параллельный участок, то:
U1=U2=U12
Следовательно, сила тока на втором резисторе равна:
I2=U2R2=I1R1R2
Сила тока на всем участке цепи равна:
I=I12=I1+I1R1R2=I1(1+R1R2)
Теперь можем вычислить ЭДС источника тока:
ε=I1(1+R1R2)(R1R2R1+R2+R3+r)
ε=1(1+31)(3·13+1+5+1)=6,75·4=27 (В)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF17511
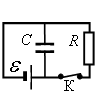 Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.
Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.
Ответ:
а) 100 нДж
б) 200 нДж
в) 100 мкДж
г) 200 мкДж
Алгоритм решения
Решение
Запишем исходные данные:
2 мкФ = 2∙10–6 Ф
Запишем закон Ома для полной цепи:
I=εR+r
Энергия конденсатора определяется формулой:
W=CU22
Напряжение внешней цепи связано с ЭЛС источника формулой:
U=ε−Ir
Используя закон Ома для полной цепи, получаем:
U=ε−εrR+r=εR+εr−εrR+r=εRR+r
Тогда энергия конденсатора через длительное время станет равной:
W=12C(εRR+r)2
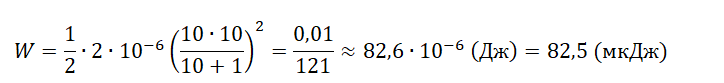
Округлим ответ до сотен и получим 100 мкДж.
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
Решение
Запишем исходные данные:
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsinα
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR
Сопротивление проводника вычисляется по формуле:
R=rlS
Тогда сила тока равна:
I=USrl
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl=BUSr=1·2,4·2·10−20,12=0,4 (Н)
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17754
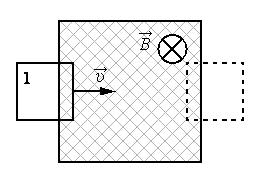 В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
Ответ:
а) 1 мА
б) 5 мА
в) 10 мА
г) 20 мА
Алгоритм решения
Решения
Запишем исходные данные:
10 см = 0,1 м
Индукционный ток, возникающий в рамке, определяется по формуле:
Ii=εiR
Закон электромагнитной индукции для движущихся проводников:
εi=vBlsinα
Отсюда индукционный ток равен:
Ii=vBlsinαR
На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:
Ii=vBlsin90°R=1·0,1·0,1·110=0,001 (А)=1 (мА)
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF22682
Алгоритм решения
Решение
Запишем исходные данные:
Сделаем рисунок. Так как препятствие квадратное, оно располагается параллельно полу, а его центр лежит на одной вертикали с точечным источником света, можем построить рисунок, наблюдая картину с одной стороны квадратного препятствия. В этом случае OE соответствует высоте потолка, EB — расстоянию от пола до препятствия, а AC — стороне квадратного препятствия. При этом тень будет иметь форму квадрата. Поэтому для нахождения ее площади достаточно найти сторону этого квадрата — DF.
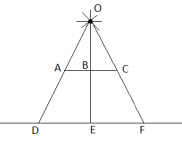
Треугольники OBC и OEF являются подобными по трем углам. Угол O у них общий. Углы B и E — прямые (так как они образованы при пересечении вертикалью двух параллельных плоскостей). А углы C и F равны как углы при параллельных прямых и секущей.
Следовательно, OB относится к OE так же, как BC относится к EF. Причем EF — половина стороны квадрата тени, поскольку треугольник DOF — равнобедренный. Это следует из того, что перпендикуляр, проведенный к основанию равнобедренного треугольника, одновременно является его биссектрисой и медианой. Следовательно, отрезок OE делит на 2 равные части DF.
Отсюда:
OBOE=BCEF
Умножим числитель и знаменатель дроби в правой части уравнения и получим:
OBOE=2BC2EF=ACDF
Причем OB можно вычислить как разность высоты потолка и расстояния от препятствия до пола:
OB=OE−BE
Получаем:
DF=OE·ACH−h=aHH−h=2·44−2=4 (м)
Это сторона квадрата тени. Чтобы найти площадь тени, нужно возвести эту величину в квадрат:
S=DF2=42=16 (м2)
Ответ: 16pазбирался: Алиса Никитина | обсудить разбор
Задание EF17685
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Ответ:
а) 0,50 м
б) 0,75 м
в) 1,25 м
г) 1,50 м
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Алгоритм решения
Решение
Запишем известные данные:
Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:
Γ=fd
f=Γd
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Γd=dFd−F
Поделим на d и выразим расстояние от предмета до линзы:
Γ=Fd−F
d=FΓ+F=14+1=1,25 (м)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18124
Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.
Ответ:
а) 5 см
б) 10 см
в) 20 см
г) 36 см
Алгоритм решения
Решение
Запишем известные данные:
Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.
Запишем формулу увеличения линзы:
Γ=Hh=fd
Отсюда расстояние от изображения до линзы равно:
f=Hdh
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Hdh=dFd−F
Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:
Hh=Fd−F
H(d−F)=hF
Hd−HF=hF
hF+HF=Hd
F(h+H)=Hd
F=Hdh+H=12·3012+6=20 (см)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18230
Дифракционная решётка с периодом 10–5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.
Алгоритм решения
Решение
Запишем исходные данные:
0,4 мкм = 0,4∙10–6 м.
3 см = 3∙10–2 м
Сделаем пояснительный чертеж:
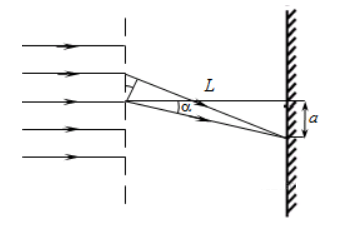
Запишем условие интерференционных максимумов дифракционной решётки:
dsinα=kλ
Из курса геометрии известно, что тангенс угла равен отношению прилежащего катета к противолежащему. Следовательно:
tanα=aL
Из условия задачи синус и тангенс этого угла равны. Следовательно:
sinα=tanα=aL
Найдём номер дифракционного максимума, который будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины:
daL=kλ
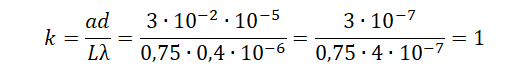
pазбирался: Алиса Никитина | обсудить разбор
👀 5.5k