Задание №25 ОГЭ по физике

Расчетная задача по механике

Задание №25 ОГЭ по физике – расчетная задача по механике. В задании не предлагаются варианты ответов. Получить ответ можно только в результате расчета по рабочей формуле, которую необходимо вывести после анализа процессов, описанных в условии задания, и применения законов механики и основных ее понятий и определений. Для решения может потребоваться использование материалов из любых ее разделов от кинематики до гидроаэромеханики. Чтобы успешно справиться с заданием, рекомендуется, в частности, четко знать все о силах, действующих в механике, повторить содержание з-нов Ньютона, сохранения энергии, сохранения импульса. Кроме того, в задании может возникнуть надобность в применении некоторых понятий термодинамики (например, об агрегатных преобразованиях вещества).

Разбор типовых вариантов заданий №25 ОГЭ по физике

Демонстрационный вариант 2019

[su_note note_color=»#defae6″]

Тело массой 100 кг поднимают с помощью троса на высоту 25 м в первом случае равномерно, а во втором – с ускорением 2 м/с2. Найдите отношение работы силы упругости троса при равноускоренном движении груза к работе силы упругости при равномерном подъёме.

[/su_note]

Алгоритм решения:
  1. Записываем краткое условие.
  2. Зарисовываем рисунок с изображением действующих на тело сил.
  3. Определяем ур-ние для силы упругости при равномерном подъеме.
  4. Находим ур-ние для силы упругости при ускоренном подъеме.
  5. Находим ур-ния для вычисления работы в обоих случаях. Находим искомое отношение. Записываем ответ.
Решение:

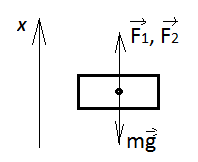
  1. Дано: m=100 кг, h=25 м, a1=0, a2=2 м/с2, А2/А1 – ?
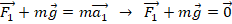
  2. По 2-му з-ну Ньютона в 1-м случае (при равномерном подъеме) 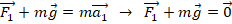. В проекции на ось Ох получим: F1–mg=0 → F1=mg.
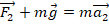
  3. По 2-му з-ну Ньютона во 2-м случае (при подъеме с ускорением) 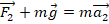. В проекции на ось Ох имеем: F2–mg=ma2 → F2=mg+ma2=m(g+a2). Проекцию ускорения а2 берем положительной, поскольку по условию движение осуществляется вертикально вверх, т.е. совпадает с направлением оси Ох.
  4. Ф-ла для вычисления работы в данном случае выглядит так: A=F·h. Отсюда: A1=F1·h=mgh, A2=F2·h=mh(g+a2). Тогда 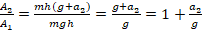. Вычислим отношение: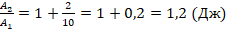

Ответ: 1,2 Дж

Первый вариант (Камзеева, № 5)

[su_note note_color=»#defae6″]

Какой путь прошел автомобиль, если известно, что при средней скорости 100 км/ч его двигатель израсходовал 30 кг бензина? Мощность автомобиля равно 46 кВт, а КПД двигателя равен 36%.

[/su_note]

Алгоритм решения:
  1. Записываем краткое условие. Переводим в СИ не соответствующие значения.
  2. Записываем ф-лу для расчета КПД (1).
  3. Выводим ф-лу для вычисления затраченной работы (2).
  4. Выводим ф-лу для определения полезной работы. Записываем ф-лу для расчета времени через путь и скорость. Объединяем полученные ур-ния (3).
  5. Ф-лы (2) и (3) подставляем в (1), выражаем искомую величину. Вычисляем значение пути. Полученный результат переводим в км.
Решение:
  1. Дано: v=100 км/ч (100:3,6≈27,78 м/с), m=30 кг, N=46 кВт (46·103 Вт), ɳ=36%, s – ?
  2. Формула для КПД двигателя имеет вид: .
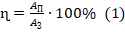  3. Затраченная работа (АЗ) в данной ситуации равна количеству теплоты, выделившейся при сгорании бензина, т.е. АЗ=Q. А поскольку при сгорании кол-во выделяющейся теплоты определяется как Q=qm, где q – уд.теплота сгорания вещества, то АЗ=qm (2). Т.к. по условию сгорает бензин, то q=4,4·107 Дж/кг.
  4. Полезную работу (АП) выразим через мощность: AП=N·t, где t – время движения машины. А время – через искомую величину пути: t=s/v. Тогда .
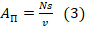  5. (2, 3 → 1): 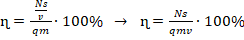. Из полученного ур-ния выразим искомую величину (путь s): 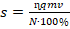. Вычислим путь: .

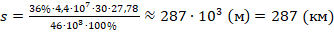Ответ: s=287 км

Второй вариант (Камзеева, № 6)

[su_note note_color=»#defae6″]

Два свинцовых шара массами m1=100 г и m2=200 г движутся навстречу друг другу со скоростями 2 м/с и 4 м/с соответственно. Чему равна кинетическая энергия шаров после их абсолютно неупругого соударения?

[/su_note]

Алгоритм решения:
  1. Записываем краткое условие.
  2. Используя з-н сохранения импульса, записываем ур-ние взаимодействия шаров до и после столкновения (в векторной форме).
  3. Преобразуем полученное векторное ур-ние в скалярную форму через проекции векторных величин.
  4. Из ур-ния (п.3) выражаем совместную скорость шаров после столкновения.
  5. Записываем ф-лу для кинетич.энергии. Подставляем в нее ур-ние, полученное для скорости (см.п.4).
  6. Вычисляем кинетич.энергию. Записываем ответ.
Решение:
  1. Дано: m1=100 г (0,1 кг), m2=200 г (0,2 кг), v1=2 м/с, v2=4 м/с, ЕК – ?
  2. Абсолютно неупругим является удар, в результате которого 2 тела начинают двигаться как единое целое (в контакте друг с другом). Это означает, что свинцовые шары, столкнувшись, далее продолжают взаимодействовать между собой. Тогда они имеют общую (одинаковую) скорость движения и, согласно з-ну сохранения импульса: .
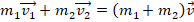  3. Шары двигаются вдоль общей прямой, которую будем считать осью и относительно которой распишем проекции векторных величин. Направим ось, например, в сторону направления движения 1-го шара с массой m1 и скоростью v1 (можно было бы использовать и противоположное направление). В этом случае получим, что проекция вектора скорости 1-го шара будет положительной, а 2-го – отрицательной. При этом проекция движения шаров после столкновения будет направлена в сторону, совпадающую с движения с шаром, имеющим больший импульс до столкновения. Поскольку у 2-го шара больше и масса и скорость, то очевидно, что вектор движения шаров после столкновения окажется сонаправленным с движением 2-го шара до столкновения, а проекция, соответственно, отрицательной. Поэтому в проекциях получим: .
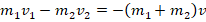  4. Из полученной ф-лы (п.3.) выразим скорость: .
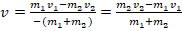  5. Кинетич.энергия шаров определяется по ф-ле: 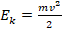, где m – суммарная масса шаров после соударения, поэтому m=m1+m2. Подставив в ф-лу для кинетич.энергии ур-ние для массы, а также для скорости (см.п.4), получим: .
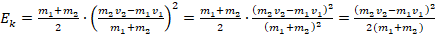  6. Вычислим кинетич.энергию:  .

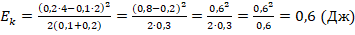Ответ: ЕК=0,6 Дж

Третий вариант (Камзеева, № 12)

[su_note note_color=»#defae6″]

Санки без трения съезжают с ледяной горки высотой 5 м с нулевой начальной скоростью. На горизонтальном участке пути они тормозят и до полной остановки проходят путь в 25 м. Чему равен коэффициент трения скольжения санок о поверхность горизонтального участка пути?

[/su_note]

Алгоритм решения:
  1. Записываем краткое условие.
  2. Анализируем условие задачи, определяем ур-ние для расчета кинетич.энергии.
  3. Связываем с кинетич.энергией величину работы, совершенной санками на горизнт.участке (1).
  4. Записываем основную ф-лу для расчета работы. Связываем ее с силой трения (2).
  5. Приравниваем ф-лы (1) и (2). Выполняем преобразования (сокращение величин), выражаем коэф-т трения.
  6. Вычисляем коэф-т трения. Записываем ответ.
Решение:
  1. Дано: h=5 м, s=25 м, μ – ?
  2. Поскольку санки съезжают с горки без трения, значит, потерь энергии при этом не происходит. Соответственно, вся потенц.энергия, которой они обладают на вершине горки (EP=mgh), согласно з-ну сохранения энергии, преобразуется к концу спуска с горки в кинетич.энергию (EK). Отсюда: EK=mgh.
  3. По горизонтальному участку санки двигаются, испытывая силу трения. Движение происходит до остановки. Это означает, что санки совершают работу, в результате которой полностью расходуется кинетич.энергия, которой они обладали в начале горизонтального участка, т.е. А=mgh (1).
  4. С другой стороны А=Fs. Здесь F – сила трения, для преодоления которой совершается работа. F=μN, где N – реакция опоры. В данном случае N=mg (по 3-му з-ну Ньютона). Получаем: F=μmg. Тогда работа равна: A=μmgs (2).
  5. (1)=(2): mgh=μmgs → h=μs → μ=h/s.
  6. Вычислим μ: μ=5/25=0,2

Ответ: μ=0,2

Текст: Базанов Даниил, 4.3k 👀