Задание №3 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
В задании №3 ЕГЭ по физике необходимо решить задачу по теме импульс и энергия. Это могут быть задания по нахождению импульса или энергии с использованием законов сохранения.
Задание ЕГЭ-Ф-ДВ2023-1
Алгоритм решения:
- Записать исходные данные.
- Записать формулу для определения проекции ускорения.
- Преобразовать формулу для решения конкретной задачи.
- Определить необходимые для вычислений величины с помощью приведенного в задании графика.
- Подставить известные величины в формулу и сделать вычисления.
Решение:
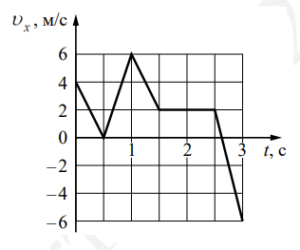
Запишем исходные данные. В задаче рассматривается движение тела в промежуток времени, ограниченный:
- Начальным значением t1 = 1 с.
- Конечным значением t2 = 1,5 с.
Проекция ускорения на ось Ox определяется по следующей формуле:
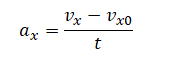
Так как по условию задачи необходимо рассчитать проекцию ускорения не за все время движения, а лишь за некоторый его промежуток, необходимо преобразовать в формуле время. Оно будет равно:
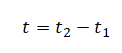
Следовательно, расчетная формула принимает вид:
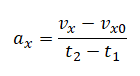
Теперь обращаемся к графику. Проекции скорости vx соответствует время t2, а проекции скорости vx0 — t1. По условию задачи t1 = 1 с. В этот момент времени vx0 = 6 м/с. По условию задачи t2 = 1,5 с. В это время vx = 2 м/с.
Подставляем данные в формулу и вычисляем проекцию ускорения:
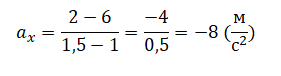
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж:

Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
 Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF17557
Алгоритм решения
Решение
Запишем исходные данные:
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19083
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать закон сохранения механической энергии.
- Записать закон сохранения применительно к задаче.
- Выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса шарика: m = 100 г.
- Высота, с которой начал падать шарик: h = 100 м.
- Энергия, потерянная за счет сопротивления воздуха: Q = 20 Дж.
100 г = 0,1 кг
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Согласно условию задачи, система не является замкнутой, так как на шарик действует сила сопротивления воздуха. Поэтому закон сохранения энергии примет вид:
Ek0 + Ep0 = Ek + Ep + Q
Шарик начал падать из состояния покоя, поэтому начальная кинетическая энергия равна нулю. В момент приземления кинетическая энергия максимальная, а потенциальная равна нулю. Поэтому:
Ep0 = Ek + Q
Потенциальная энергия определяется формулой:
Ep0 = mgh
Следовательно:
mgh = Ek + Q
Отсюда кинетическая энергия шарика в момент перед падением на землю равна:
Ek = mgh – Q = 0,1∙10∙100 – 20 = 80 (Дж)
Ответ: 80pазбирался: Алиса Никитина | обсудить разбор
Задание EF17731
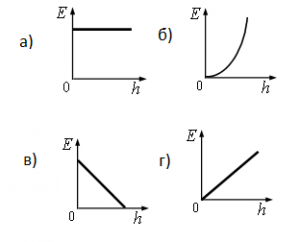 Какой из графиков, приведённых на рисунке, показывает зависимость полной энергии Е тела, брошенного под углом к горизонту, от его высоты h над Землёй? Сопротивлением воздуха пренебречь.
Какой из графиков, приведённых на рисунке, показывает зависимость полной энергии Е тела, брошенного под углом к горизонту, от его высоты h над Землёй? Сопротивлением воздуха пренебречь.Алгоритм решения
- Записать закон сохранения энергии.
- Установить зависимость полной механической энергии от высоты.
- Найти тип графику, соответствующий выявленной зависимости.
Решение
Запишем закон сохранения механической энергии:
E = const
Полная механическая энергия тела равна:
E = Ek + Ep
Исходя из закона, сумма потенциальной и кинетической энергии в начальный момент движения тела равно сумме потенциальной и кинетической энергии в конечный момент времени:
Ek0 + Ep0 = Ek + Ep
Так как полная механическая энергия не меняется с течением времени, ее графиком должна быть прямая, параллельная оси времени. Поэтому верный ответ — а.
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF22589
Тело, брошенное вертикально вверх от поверхности Земли, достигло максимальной высоты 20 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
Ответ:
а) 4,5 м/с
б) 10 м/с
в) 20 м/с
г) 40 м/с
Алгоритм решения
Решение
Из условия задачи известна только высота h = 20 м.
Закон сохранения механической энергии для замкнутой системы:
Ek0 + Ep0 = Ek + Ep = const
Тело изначально находилось на поверхности Земли, поэтому его начальная потенциальная энергия равна нулю. Но кинетическая энергия в момент броска была максимальной. В верхней точке траектории скорость тела нулевая, поэтому кинетическая тоже равна нулю. Но потенциальная энергия в этот момент времени максимальна.
Поэтому:
Ek0 = Ep
Кинетическая и потенциальная энергии определяются формулами:
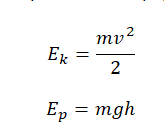
Приравняем их:
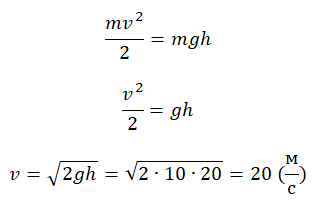
pазбирался: Алиса Никитина | обсудить разбор
👀 11.6k
у вас ошибка в ЗСИ: должно быть м1*в1+м2*в2=м1*в1(штрих)+м2*в2(штрих)