Задание №11 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 2 Среднее время выполнения: 3 мин.
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
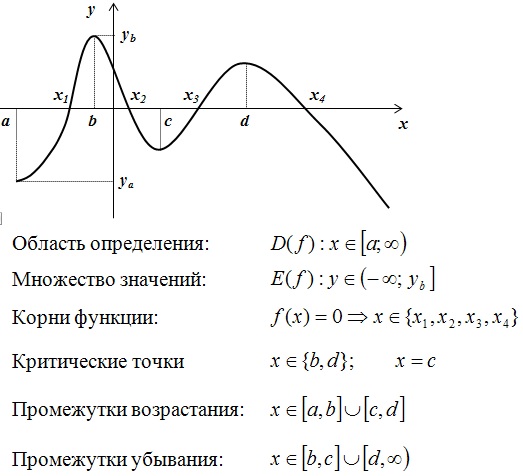
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
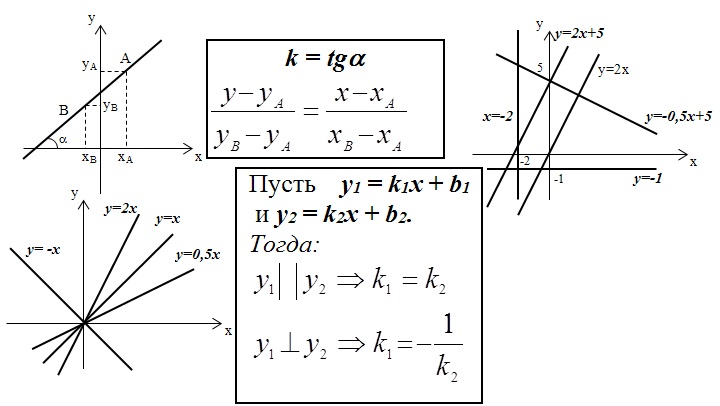
Рассмотрим случай квадратичной функции:
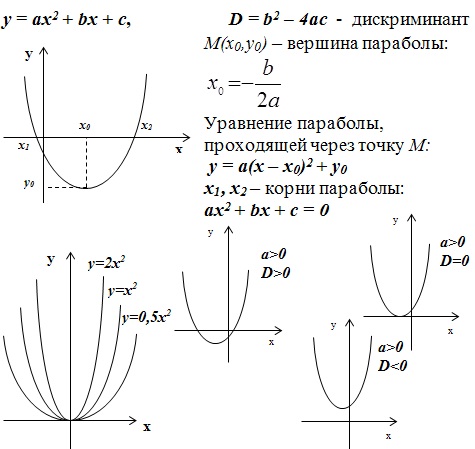
Также вспомним, что такое коренная функция и модуль:
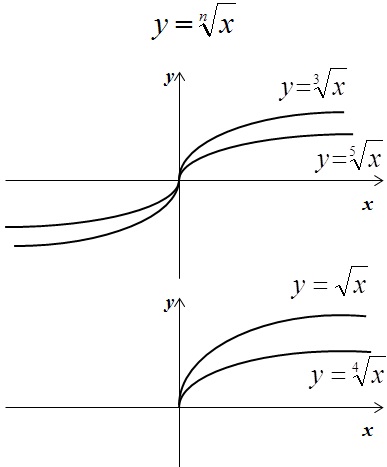
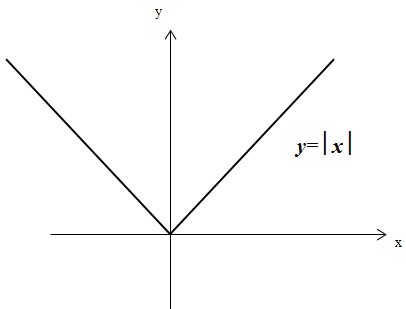
Задание 11OM21R
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
 В таблице под каждой буквой укажите соответствующий номер.
Ответ:
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
| А | Б | В |
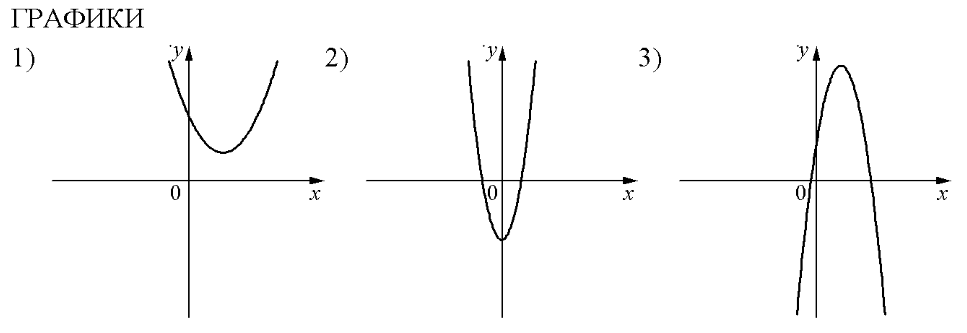
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
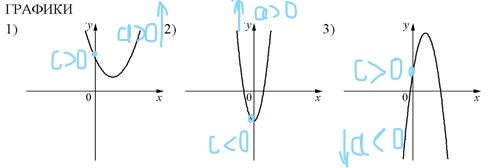
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 — это график №1
Б) а<0; с>0 — это график №3
В) а>0, с<0 – это график №2
| А | Б | В |
| 1 | 3 | 2 |
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1106o
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
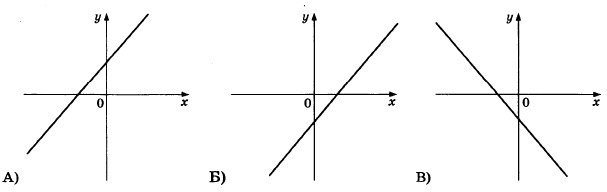
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213pазбирался: Базанов Даниил | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3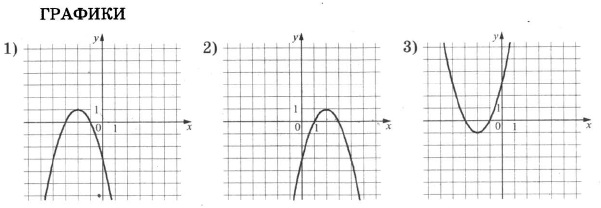
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123pазбирался: Базанов Даниил | обсудить разбор
Задание OM1104o
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
Ответ:
А 1
Б 3
В 2
Ответ: 132pазбирался: Базанов Даниил | обсудить разбор
Задание OM1103o
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231pазбирался: Базанов Даниил | обсудить разбор
Задание OM1102o
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231pазбирался: Базанов Даниил | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
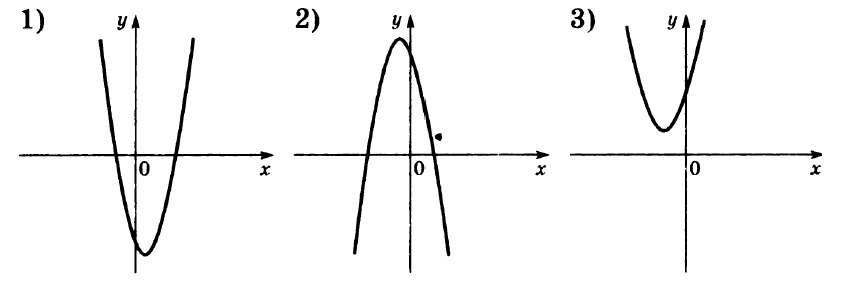
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321pазбирался: Базанов Даниил | обсудить разбор
👀 46.2k
А за что отвечает коэффициент b ?
Коэффициент b отвечает как за сдвиг по оси X и Y, так и за «крутизну» ветвей параболы. Другими словами, данный коэффициент влияет практически на все характеристики (кроме направления ветвей), однако в заданиях этого типа про него никогда не спрашивают, поэтому можно о нем не задумываться. Влияние сдвига по оси Y мало в сравнении с коэффициентом с, поэтому именно с определяет сдвиг относительно оси Y.
А на конкретном примере f(х)= 2х^2-5х+3, с больше нуля, а вершина ниже оси х?
Это единственный сайт на котором всё ясно и понятно. Очень благодарна создателям
Вы всё понятно объяснили.Спасибо!
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c 0, то пересекает выше оси ОХ
если c < 0, то пересекает ниже оси ОХ
Пятый вариант решён неверно. Должно быть 231
Вариант 4 решен неверно, так как при подстановке точек, которые лежат на графике 2 в уравнение А, равенство не выполняется, чего быть не может! Ответ 123
Спасибо, исправили, добавили новое решение!