Задание №14 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 2 Среднее время выполнения: 2 мин.
В 14-ом задании мы сталкиваемся с прогрессиями - общими понятиями. Ответом в задании 14 является целое число или конечная десятичная дробь.
Теория к заданию №14
Начнем теоретическую справку об определениях прогрессий.
Арифметическая прогрессия:
Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.
an+1 = an + d
где d – разность прогрессии
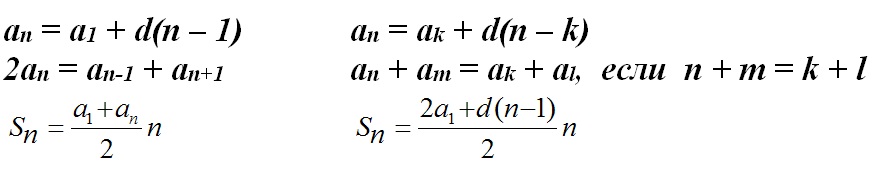
Геометрическая прогрессия:
Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.
bn+1 = bn q
где q – знаменатель прогрессии
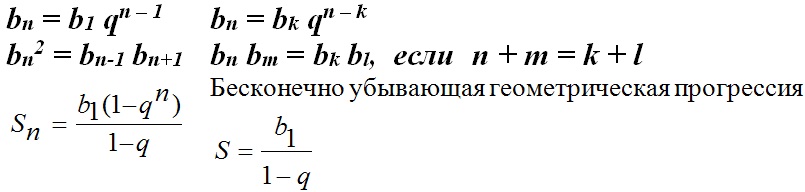
Задание OM1420225
Рассмотрим решение данной задачи самым простым способом. Для этого разберем, что происходило с изотопами. Имеем один изотоп А массой 400 мг. Через каждые 9 минут половина его атомов преобразуется в атомы второго изотопа Б (то есть первый отдает второму свою половинку каждые 9 минут). Нам надо узнать массу этого второго изотопа Б через 36 минут. Запишем это решение в виде таблицы:
| Время/мин | Изотоп А/мг | Изотоп Б/мг |
| 0 — это нач.этап | 400 | 0 |
| 9 мин | 400:2=200 | 200 |
| 9+9=18 | 200:2=100 | 200+100=300 |
| 18+9=27 | 100:2=50 | 300+50=350 |
| 27+9=36 | 50:2=25 | 350+25=375 |
Видим, что через 36 минут масса изотопа Б стала 375 мг.
Ответ: 375pазбирался: Базанов Даниил | обсудить разбор
Задание OM1420224
Рассмотрим простой способ решения данной задачи. Итак, выпишем, что имеем по условию и что надо узнать. Имеем изотоп массой 320 мг, затем его масса уменьшается в 2 раза каждые 8 минут. Найти надо его массу через 48 минут. Удобнее записать это в виде таблицы, просчитывая сначала время (левый столбец), прибавляя по 8 мин и дойдя до 48 мин, как сказано в условии, а затем в правом столбце просчитываем массу, уменьшая её в 2 раза:
| Время/мин | Масса/мг |
| 0 — это нач.этап | 320 |
| 8 | 320:2=160 |
| 8+8=16 | 160:2=80 |
| 16+8=24 | 80:2=40 |
| 24+8=32 | 40:2=20 |
| 32+8=40 | 20:2=10 |
| 40+8=48 | 10:2=5 |
Значит, через 48 минут масса изотопа станет 5 миллиграммов.
Ответ: 5pазбирался: Базанов Даниил | обсудить разбор
Задание OM1420223
Выпишем, что мы имеем по условию задачи в левый столбец, а в правый запишем то, что из этого следует
| Известно | Решение |
| Подача и первые 5 минут – 159 руб | — |
| Стоимость с 6 по 15 минуту – 80 рублей
Стоимость с 6 по 25 минуту – 160 рублей. |
Разница во времени 10 минут стоит 80 руб |
| Значит, 1 минута стоит 8 руб (80:10=8) | |
| 1 час — ? руб | 1 час=60 мин; убираем 5 минут, которые включены в подачу машины, значит, надо найти стоимость 55 минут: 55•8=440 руб
Прибавляем стоимость подачи: 440+159=599 рублей |
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1420222
Определим, к какой последовательности относится наша задача. По условию имеем, что после каждого следующего отскока от асфальта подлетал на высоту в 2 раза меньше предыдущей. Это геометрическая прогрессия. Теперь выпишем, что известно по условию и определим, что надо найти: первый член прогрессии b1=400, знаменатель q=1\2, n – количество отскоков, значит, найти надо n при bn<20.
Подставим в формулу n-ого члена геометрической прогрессии наши данные:
bn=b1qn-1=400∙(12)n−1<20
Разделим обе части неравенства на 400: (12)n−1<120
Будем рассматривать случаи, начиная с n=3: (12)3−1<120; (12)2<120; (14)<120 неверно
При n=4: (12)4−1<120; (12)3<120; (18)<120 неверно
При n=5: (12)5−1<120; (12)4<120; (116)<120 неверно
При n=6: (12)6−1<120; (12)5<120; (132)<120 верно. Следовательно, после 6 отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см.
К данной задаче можно сделать проверку, а также она является простейшим способом для её решения. Рассмотрим этот способ:
1 отскок – 400 см
2 отскок – 200 см (разделили на 2, так как по условию сказано, что с каждым отскоком высота уменьшалась в 2 раза)
3 отскок – 100 см
4 отскок – 50 см
5 отскок – 25 см
6 отскок – 12,5 см, а это меньше, чем 20 см, как требуется в условии. Поэтому пишем в ответ число 6.
Ответ: 6pазбирался: Базанов Даниил | обсудить разбор
Задание OM1420221
Из условия задачи видно, что имеем дело с арифметической прогрессией, так как сказано, что в каждом следующем на 2 места больше, чем в предыдущем.
Выписываем, что нам известно и определяем, что нужно найти: всего 12 рядов, значит n=12; в первом ряду 18 мест, значит, а1=18; так как в каждом последующем ряду мест на 2 больше, то разность арифметической прогрессии d=2. Надо найти, сколько всего мест в амфитеатре, т.е. найти сумму арифметической прогрессии S12.
Для нахождения суммы имеем формулу Sn=a1+an2×n, то есть для нашей задачи S12=a1+a122×12. У нас нет а12, найдем его по формуле n-ого члена арифметической прогрессии: a12=a1+d(n-1)=18+2(12-1)=18+22=40. Подставим данные в формулу суммы:
S12=18+402×12=348
Следовательно, 348 мест всего в амфитеатре.
Проверка: можно проверить решение следующим способом, просто прибавляя по 2 места в каждый ряд до 12-ого, а затем сложить количество мест. Записать можно так: 18+20+22+24+26+28+30+32+34+36+38+40=348. Этим же способом, кстати, можно решить задачу, если от волнения забыли про арифметическую прогрессию.
Ответ: 348pазбирался: Базанов Даниил | обсудить разбор
Задание 14OM21R
Можно решить данную задачу логическим путем, т.е. без формулы. Так как начальная температура была -6, а потом уменьшалась на 8 градусов в течение 6 минут, то можно сделать следующее:
-6-8=-14 через 1 минуту
-14-8=-22 через 2 минуты
-22-8=-30 через 3 минуты
-30-8=-38 через 4 минуты
-38-8=-46 через 5 минут
-46-8=-54 через 6 минут
Значит, наш ответ -540С
Вторым способом является решение по формуле n-ого члена арифметической прогрессии, которая есть также и в справочном материале, т.е. an=a1+d(n – 1). В данном случае a1=-6; d=-8, n=7 (так как ЧЕРЕЗ 6 минут). Подставим значения в формулу: a7=-61-8(7 – 1). Вычислим: a6=-6-8∙5=-6-48=-54.
Ответ: -54pазбирался: Базанов Даниил | обсудить разбор
Задание OM1407
Содержание данной задачи говорит нам о том, что здесь есть арифметическая прогрессия, так как число жителей города возрастало на одну и ту же величину.
Рассмотрим данные:
2008 г – 38100 человек
2012 г — ? человек
2016 г. – 43620 человек
Удобно решить данную задачу способом по формуле связи между любыми двумя членами арифметической прогрессии: d=an−akk−n , где k>n. Число d (разность прогрессии) будет являться ежегодным приростом населения.
Итак, можно вычислить прирост населения с 2008 по 2016 ежегодно:
(43620 – 38100):(2016 – 2008)= 5520:8=690 человек.
Теперь можно найти, сколько человек проживало в конце 2012 года.
38100+690(2016 – 2012)= 40860 человек
Ответ: 40860pазбирался: Базанов Даниил | обсудить разбор
Задание OM1406
Анализируя содержание задачи, можно сказать, что мы имеем дело с геометрической прогрессией, так как после первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8, а это значит, что с каждой последующей минутой количество очков удваивается. То есть знаменатель геометрической прогрессии q равен 2, b1=2 по условию (после 1 минуты 2 очка). Так как очки суммируются, то будем использовать формулу суммы n первых членов геометрической прогрессии Sn=b1(qn−1)q−1, где Sn>30000, так как для перехода на следующий уровень ему нужно набрать не менее 30000 очков.
Подставляем наши данные в формулу: 2(2n−1)2−1>30000
Упрощаем выражение: так как в знаменателе дроби получается 1, то получим 2(2n-1)>30000; делим обе части на 2: 2n-1>15000; переносим 1 в правую часть и получим: 2n>15001. Теперь надо подобрать число n, при котором будет верно наше неравенство. Делать это можно постепенно, возводя 2 в степени, а можно запомнить, что 210=1024. Тогда легко будет добраться до числа, которое меньше 15001, а это 214=16384, где 16384<15001. Следовательно, наш ответ 14 минут.
Ответ: 14pазбирался: Базанов Даниил | обсудить разбор
Задание OM1405
В содержании задачи есть фраза, что акции дорожали ежедневно на одну и ту же сумму, следовательно, имеем арифметическую прогрессию. Итак, определяем, что известно: в 7-й день акция стоила 777 рублей, это а7=777; в 12-й день – 852 рубля, это а12=852. Известно, что акции дорожали 25 дней, а найти надо стоимость акции в последний, т.е. в 25-ый день, значит, будем искать а25.
1 способ:
В данной арифметической прогрессии нет первого члена, не идет речь про сумму, поэтому воспользуемся формулой аn=ak+d(n – k), где n>k. Числа n и k – это порядковые номера. Составим формулу для наших данных и подставим в неё значения: а12=а7+d(12-7); 852=777+d(12 – 7). Упростим выражение и найдем разность d, 852–777= d(12 – 7); 75= d∙5; отсюда d=75:5=15. Итак, мы нашли, что акции ежедневно дорожали на 15 рублей.
Теперь, зная число d, мы можем найти а25 через, например, а12, используя всё ту же формулу. Получаем: а25=а12+d(25-12); а25=852+15(25-12)=852+15∙13= 852+195=1047. Значит, 1047 рублей стоила акция в последний день.
2 способ:
Можно решить данную задачу другим способом по формуле связи между любыми двумя членами арифметической прогрессии: d=an−akk−n , где k>n. Составим формулу для наших а12 и а7, а затем подставим в нее данные: d=a12−a712−7; d=852−77712−7=15. Теперь по этой же формуле найдем а25, связывая его с а12: d=a25−a1225−12; 15=a25−85213; найдем отсюда а25, а25=15∙13+852=1047.
Ответ: 1047pазбирался: Базанов Даниил | обсудить разбор
Задание OM1404
В условии задачи встречаются слова, что норма увеличивалась на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой а1=6, так как в первый день перевезли 6 тонн. Далее, известно, что вся работа была выполнена за 11 дней, значит число n=11. Так как масса всего щебня равна 176, то это число является суммой нашей прогрессии, т.е. S11=176. Требуется найти, сколько тонн было перевезено в последний день, а он – 11, значит, найти надо а11.
Итак, если нам встретилась сумма арифметической прогрессии, значит, нам надо воспользоваться формулой суммы n первых членов арифметической прогрессии Sn=а1+аn2∙n, куда мы и подставим все данные: 176=6+а112∙11.
Разделим обе части на 11, получим 16= 6+а112 ; умножим 16 на 2 (правило пропорции): 32=6+а11. Отсюда найдем а11=32–6=26. Итак, мы нашли, что 26 тонн щебня было перевезено в последний день.
Ответ: 26pазбирался: Базанов Даниил | обсудить разбор
Задание OM1403
Из содержания данной задачи видно, что время процедуры увеличивалось с каждым днем на одно и то же количество времени – на 15 минут, следовательно, это арифметическая прогрессия. Так как в первый день курс был 15 минут, то а1=15; так как время ежедневно увеличивалось на 15 минут, то значит разность d=15; зная, что продолжительность процедуры должна достигнуть 1 ч 15 мин, т.е. достигнуть 75 минут (1 час=60 мин, плюс 15 минут), то это число 75 и будет являться n членом арифметической прогрессии. Требуется найти, в какой по счету день продолжительность процедуры достигнет этих 75 минут, т.е. найдем число n.
Теперь берем формулу n члена арифметической прогрессии аn=a1+d(n – 1) и подставляем в неё наши данные: 75=15+15(n – 1); упростим данное выражение: 75-15=15(n – 1); 60=15(n – 1); разделим на 15 обе части: 4=n – 1; найдем отсюда, что n=5. Таким образом, на пятый день продолжительность процедуры достигнет 75 минут.
Ответ: 5pазбирался: Базанов Даниил | обсудить разбор
Задание OM1402
Анализируя содержание задачи, мы видим, что улитка проползала ежедневно на одно и то же расстояние меньше, чем в предыдущий день. А это значит, что имеем арифметическую прогрессию. По условию определяем данные: так как в первый и последний дни она проползла 7,5 м, то имеем, что а1+аn=7,5. Так как расстояние между деревьями равно 60 м, то имеем сумму n первых членов прогрессии, т.е. Sn=60. Так как найти надо количество дней, которое она потратила на весь путь, то искомым числом будет число n.
Зная формулу суммы n первых членов арифметической прогрессии
Sn=а1+аn2∙n, имеем 60=7,5 ∙ n2. Отсюда находим n, умножая сначала 60 на 2 (по определению пропорции), затем 120 делим на 7,5 и получаем, что n=16. Таким образом, улитка потратила на весь путь 16 дней.
Ответ: 16pазбирался: Базанов Даниил | обсудить разбор
Задание OM1401
При анализе содержания задачи мы видим, что каждую минуту количество осадка увеличивается на одно и то же число, на 0,2 г. А это значит, что имеем арифметическую прогрессию, в которой первый член равен 0,2, так как по условию в первую минуту образовалось 0,2 г осадка. Разность арифметической прогрессии равна также 0,2, так как каждую минуту на это количество увеличивается количество осадков. Найти нужно седьмой член последовательности.
Итак, имеем а1=0,2; d=0,2. Ищем а7. По определению n-ого члена арифметической прогрессии имеем формулу аn=a1+d(n – 1). Подставим в нее наши данные: а7=a1+d(7 – 1)=0,2+0,2·6=1,4
Ответ: 1,4pазбирался: Базанов Даниил | обсудить разбор
Задание OM1206o
Сумму произвольного кол-ва членов геометрич.прогрессии будем искать по формуле:
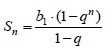
1-й член прогрессии известен из условия и равен b1=1512. Требуемое число членов n=4.
Знаменатель прогрессии найдем как частное двух соседних членов прогрессии (2-го и 1-го или 3-го и 2-го и т.д.). Найдем его так:
![]()
По условию b2=–252, b3=42, поэтому
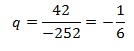
Отсюда получаем:
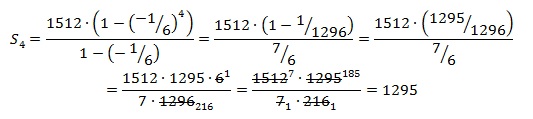
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1205o
b1=–2, bn+1=2bn.
Найдите b7.Искомый 7-й член прогрессии b7 будем искать по формуле:
b7=b1·q6. (1)
Здесь b1 по условию дано, а знаменатель q нет. Но его можно определить, исходя из определения этой величины. Согласно определению, q=bn+1/bn. Используя второе условие задачи, получим, что q=2.
Теперь используем 1-е условие задачи (b1=–2) и найдем искомую величину по формуле (1):
b7=–2·26=–2·64=–128.
Ответ: -128pазбирался: Базанов Даниил | обсудить разбор
Задание OM1204o
В данном задании нас проверяют на знание формулы арифметической прогрессии:
![]()
где n — номер члена прогрессии, d — разность, а а1 — первый член.
Решение:
Подставим в общую формулу известные из условия значения:
d = 4,
а1 = 6,
n = 15,
получим:
a15 = 6 + (15 — 1) • 4
вычислив, получаем значение 15 члена:
a15 = 62
Ответ: 62pазбирался: Базанов Даниил | обсудить разбор
Задание OM1203o
Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:
an = a1 + (n-1) • d
В нашем случае:
a1 = 10
d = 6 — 10 = -4
Подставляем значения в формулу:
a101 = 10 + (101-1) • (-4) = -390
Ответ: -390pазбирался: Базанов Даниил | обсудить разбор
Задание OM1202o
Выписано несколько последовательных членов геометрической прогрессии:
-1, x, -49, -343, ….
Найдите x.
Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:
-343 / -49 = 7
Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.
x = -49 / 7 = -7
Ответ: -7pазбирался: Базанов Даниил | обсудить разбор
Задание OM1201o
Дана арифметическая прогрессия a(n) в которой
a (3) = 6,9
a (16) = 26,4
Найдите разность прогрессии.
Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).
Находим разницу между значениями a (3) и a (16):
a (3) — a (16) = 26,4 — 6,9 = 19,5
Находим количество членов:
16 — 3 = 13
Находим разность прогрессии:
19,5 / 13 = 1,5
Ответ: 1,5pазбирался: Базанов Даниил | обсудить разбор
👀 32.7k
почему 2 часть отсутствует пожалуйста доделайте если это можно в ближайшее время. это важно
почему 2 части нет это самые трудные задания если это возможно пожалуйста укажите 2 часть тоже .заранее спасибо
Спасибо вам Большое! Вы очень выручили меня)
Спасибо Вам огромное! Вы даже не представляете, как вы помогли мне.Спасибо ещё раз!
СПАСИБИЩЕ ГРОМАДНОЕ!! ТОТ ЧЕЛОВЕЧИЩЕ, КОТОРЫЙ ВСЕ ЭТО ПИСАЛ, ЗНАЙТЕ, ЧТО ВЫ З О Л О Т О!