Задание №7 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 3 мин.
Седьмое задание ОГЭ по математике проверяет знания в области представления чисел, положение одних чисел относительно других. Задания могут сводится к переводу одного формата чисел в другой, например перевод обыкновенной дроби в десятичную, приблизительное вычисление корня или определение знака выражения, если известно положение на координатной прямой.
Теория к заданию №7
Для того, чтобы переводить дроби из обыкновенного вида в десятичный, необходимо выполнить деление столбиком.
Для успешного вычисления примерного значения корня достаточно иметь представления о вычисляемых подкоренных выражениях, а для этого необходимо хорошо знать таблицу квадратов натуральных чисел!
Таблица квадратов натуральных чисел
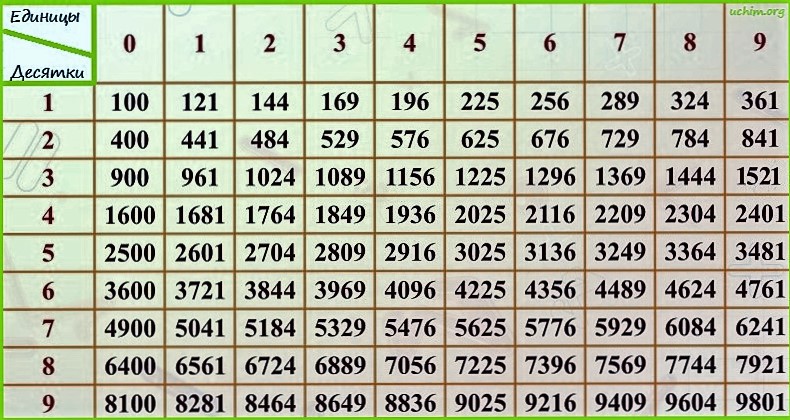
В заданиях на определение знака выражения я рекомендую подставлять числа и вычислять выражение — подробная инструкция по этому методу изложена в третьем варианте.
Задание 7OM21R
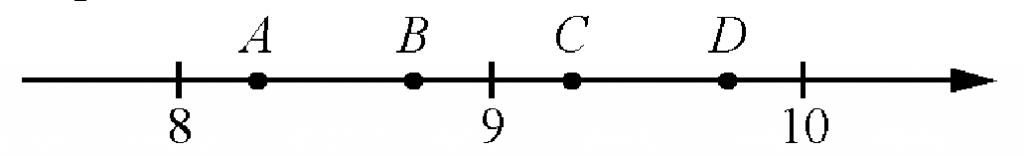 Одна из них соответствует числу 10713. Какая это точка?
Одна из них соответствует числу 10713. Какая это точка?
- точка А
- точка В
- точка С
- точка D
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.
Ответ: 1pазбирался: Базанов Даниил | обсудить разбор
Задание OM0706o
На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.
Какой точке соответствует число -0,304?
1) А 2) В 3) С 4) DСформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304<–0,201<–0,012.
В итоге имеем возрастающий ряд: –0,304; –0,201; –0,012; 0,021.
Поскольку стрелка положительного направления на координатной прямой направлена вправо, то А<B<C<D. Следовательно, А=–0,304; В=–0,201; С=–0,012; D=0,021. Значит, числу –0,304 соответствует точка А.
Ответ: Apазбирался: Базанов Даниил | обсудить разбор
Задание OM0705o
Одно из чисел ![]() отмечено на прямой точкой.
отмечено на прямой точкой.
Какое это число?
![]()
Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
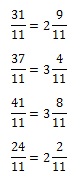
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
Ответ: 31/11pазбирался: Базанов Даниил | обсудить разбор
Задание OM0704o
На координатной прямой отмечена точка А:
![]()
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
- 181/16
- √37
- 0,6
- 4
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 — можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 — самое близкое значение, из которого вычисляется квадратный корень — это 36, значит √37 — это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 — это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
Ответ: √37pазбирался: Базанов Даниил | обсудить разбор
Задание OM0703o
На координатной прямо отмечены числа a и b:
![]()
Какое из приведенных утверждений для этих чисел неверно:
- ab²<0
- a — b > 0
- a + b < 0
- ab < 0
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b < 0, так как расположено слева. К тому же, b значительно более удалено от ноля, а значит больше по модулю.
Для удобства, исходя из вышеизложенных рассуждений, примем a = 1, а b = -2.
Теперь подставим значения в данные неравенства:
- ab²<0
1 • (-2)² = 4 > 0
Значит, утверждение неверно.
- a — b > 0
1 — (-2) = 3 > 0
Утверждение верно.
- a + b < 0
1 + (-2) = -1 < 0
Утверждение верно.
- ab < 0
1 • (-2) = -2 < 0
Утверждение верно.
Следовательно, правильный ответ первый.
Ответ: ab²<0pазбирался: Базанов Даниил | обсудить разбор
Задание OM0702o
Какое из данных чисел принадлежит промежутку [ 6 ; 7 ] ?
- √6
- √7
- √38
- √50
Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.
- Рассмотрим √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
- Рассмотрим √7. Ситуация аналогична √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
- Рассмотрим √38. Ближайшее вычисляемое число меньше 38 — 36, √36 = 6, ближайшее вычисляемое число больше 38 — 49, √49 = 7, значит √38 лежит между 6 и 7
- Рассмотрим √50. Ближайшее вычисляемое число меньше 50 — 49, √49 = 7, ближайшее вычисляемое число больше 50 — 64, √64 = 8, значит √50 лежит между 7 и 8
Значит, нам подходит третий вариант ответа — √38.
Ответ: √38pазбирался: Базанов Даниил | обсудить разбор
Задание OM0701o
Какое из следующих чисел заключено между числами 8/3 и 11/4 ?
- 2,7
- 2,8
- 2,9
- 3
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
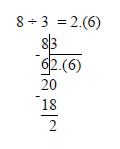
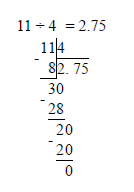
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
Ответ: 2,7pазбирался: Базанов Даниил | обсудить разбор
👀 30.3k
Здраствуйте …вы можете по другому объяснить разбор 1примера ? Я не очень поняла …заранее спасибо
1 пример вообще не понятен, откуда взялось 2, 6666…? В принципе, вообще ничего не понятно.
А что тут сложного? Как и написано, выполняйте деление 8 на 3 столбиком, вот и получите 2,6666… это бесконечная периодическая дробь. Так же получаете 2,75, только тут дробь конечная. А дальше просто смотрите, какое число больше первого, но меньше второго.
Я 3 вариан вообще не понимаю в первом 4>0 неверно,а 3>0 верно.объясните пожалуйста
Потому что там по условию нужно проверить правильность утверждений, в условии написано меньше ноля, а при подстановке получаем 4, что больше нуля, значит утверждение неверное.
А в следующем в условие было БОЛЬШЕ, что СОВПАДАЕТ с нашими вычислениями, поэтому этот ответ ВЕРЕН. 🙂
блин почему все пишут тип ничего не понятно?!
всё довольно понятно просто вы понимать этого не хотите,и если вы зашли на сайт где объясняют а не тупо решают то зачем вы на нём сидите?
как по мне всё хорошо объяснии только вот теперь заучить надо :3
Ну тупо ложки которые , не могут понять знак меньше и больше, это дикость уже..