Задание №8 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 3 мин.
Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями. При выполнении задания №8 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений. В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости. Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №8
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
Кроме этого, нам понадобятся формулы сокращенного умножения:
Квадрат суммы
(a + b)2 = a2 + 2ab + b2
Квадрат разности
(a — b)2 = a2 — 2ab + b2
Разность квадратов
a2 – b2 = (a + b)(a – b)
Куб суммы
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Сумма кубов
a3 + b3 = (a + b)( a2 — ab + b2)
Разность кубов
a3 – b3 = (a – b)( a2 + ab + b2)
Правила операций с дробями:

Задание 8OM21R
(3∙8)737∙85
В числителе дроби возведем в степень каждый множитель:
(3∙8)737 ∙85=37∙8737∙85
Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.
(3∙8)737 ∙85=37∙8737∙85=82=64
Ответ: 64pазбирался: Базанов Даниил | обсудить разбор
Задание OM1306o
Найдите значение выражения:
![]()
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
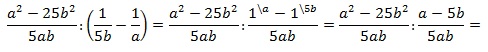
теперь переходим от деления дробей к их умножению:
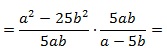
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
![]()
сокращаем выражение на (a–5b):
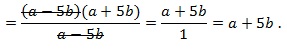
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
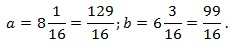
Подставим полученные значения в выражение и найдем конечный результат:
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1305o
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
![]()
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
![]()
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
![]()
Подставляем числовое значение для х в полученное выражение и находим результат:
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1304o
Найдите значение выражения

где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a — 9b²
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25pазбирался: Базанов Даниил | обсудить разбор
Задание OM1303o
Найдите значение выражения:

при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
![]()
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
Ответ: -0,4pазбирался: Базанов Даниил | обсудить разбор
Задание OM1302o
Найдите значение выражения:

при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Сокращаем (a-b):

И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5pазбирался: Базанов Даниил | обсудить разбор
Задание OM1301o
Найдите значение выражения: (x + 5)2 - x (x- 10) при x = - 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5)2 — x (x — 10) = x2 + 2 • 5 • x + 25 — x2 + 10x
Затем приведем подобные слагаемые:
x2 + 2 • 5 • x + 25 — x2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
Ответ: 24pазбирался: Базанов Даниил | обсудить разбор
Задание OM0807o
![]()
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
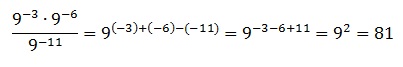
pазбирался: Базанов Даниил | обсудить разбор
Задание OM0806o
Найдите значение выражения:
В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:
![]()
По аналогии извлекаем и 2-й корень:
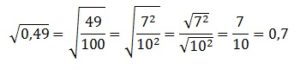
В итоге получаем:
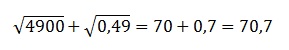
pазбирался: Базанов Даниил | обсудить разбор
Задание OM0805o
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание OM0804o
Какое из данных ниже чисел является значением выражения?


Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
16 — 14 = 2
Суммарно наши действия выглядят так:

pазбирался: Базанов Даниил | обсудить разбор
Задание OM0803o
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
- √810
- √8,1
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: √0,81pазбирался: Базанов Даниил | обсудить разбор
Задание OM0802o
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
- 3√5
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
- 2√11
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
- 2√10
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
- 6,5
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
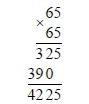
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый.
Ответ: 3√5pазбирался: Базанов Даниил | обсудить разбор
Задание OM0801o
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2pазбирался: Базанов Даниил | обсудить разбор
👀 41.6k
Что значит рвциональные и иррациональные?
там же объяснено читай внимательно если сможешь извлечь из корня то оно рационально
Здравствуйте!Спасибо большое за ваши разборы решений!Не могли бы вы оповестить,когда будет разбор демонстр. варианта 2017 года?Возникли проблемы с заданием 3.Как понять,какое число рационально ?
Хорошо, в ближайшее время постараюсь разобрать. Более того, планирую запись видеоуроков по разборам заданий. Спасибо за отзыв!
Сложно
Я троешница и не знаю как решать
спасибо
Что конкретно Вам непонятно?
((((((
Спасибо за объяснение, очень помогло
спасибо за объяснения очень хороший сайт!!!!!! завтра пробник готовлюсь на вашем сайте.
Готовлюсь к экзаменам по вашему сайту , посмотрим что из этого выйдет , ну так вроде более менее понятно. Спасибо))
Спасибо большое за такой сайт вот алгебру не сдала буду передавать вот и готовлюсь))
как вы так раскрыли скобки? в 5 примере