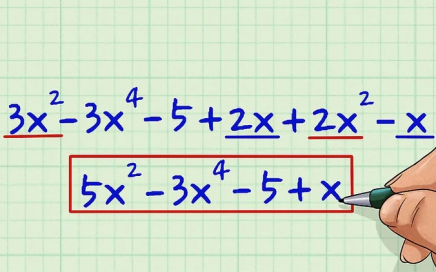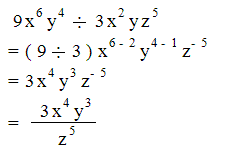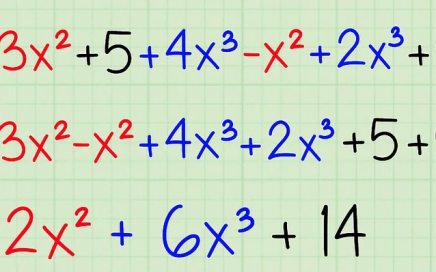Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби: 4a−9b+39a−4b+3..=5 5(9а – 4b + 3)=4a – 9b+3 Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные): 45a – 20b +15 =4a – […]
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю: теперь переходим от деления дробей к их умножению: затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов: сокращаем выражение на (a–5b): Представим числовые значения для a и b […]
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению: далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы): теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду: Подставляем числовое значение для х […]
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе: 9b² + 5a — 9b² Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь: […]
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно: Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель: 5 y — (3 x + […]
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки: (x + 5)2 — x (x — 10) = x2 + 2 • 5 • x + 25 — x2 + 10x Затем приведем подобные слагаемые: x2 + 2 • 5 • x + 25 — x2 + 10x = 20 x + 25 Далее подставим x из условия: 20 x + 25 = 20 • […]
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b < 0, так как расположено слева. К тому же, b значительно более удалено от ноля, а значит больше по модулю. Для удобства, исходя из вышеизложенных рассуждений, примем a = 1, а b […]
Определение Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения. Примеры алгебраических дробей: Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям. Сокращение алгебраической дроби Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на […]
Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения. Квадрат суммы и квадрат разности Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения: (a+b)2=a2+2ab+b2 Квадрат разности двух выражений равен квадрату первого […]
Что такое многочлен? Многочлен – это сумма одночленов. Одночлены, которые составляют многочлен, называют членами данного многочлена. Если многочлены состоят из двух или трех слагаемых, то их можно называть двучленами или трехчленами соответственно. Пример №1. –12х6+ 35с данный многочлен состоит из двух слагаемых – одночленов, таких как: –12х6 и 35с. Еще такой многочлен можно называть двучленом. […]
Что такое одночлен? Одночлен – это простейшее алгебраическое выражение, которое состоит из произведения чисел, переменных и их степеней. Никаких других действий одночлен не имеет. Числовой множитель у одночлена называется коэффициентом. Пример №1. Рассмотрим примеры одночленов. 5ху это одночлен с коэффициентом, равным 5 -2,76mn2 у этого одночлена коэффициент равен -2,7 15abc здесь коэффициент равен 15 ¾xy5 […]
Что такое числовое выражение? Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок. Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения. 256 : 2 + 315×5 (181 – 19)×6 – 121:11 13,5 + 16 – […]