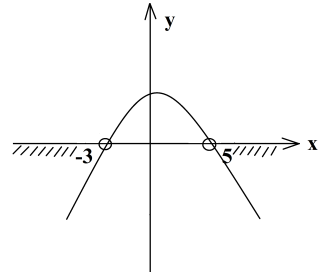
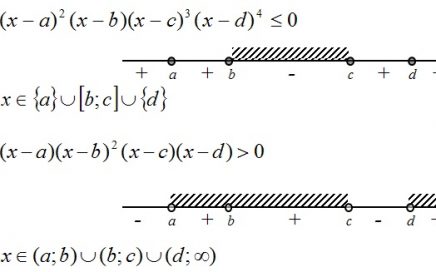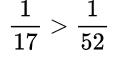Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль: (х−5)2−√7(х−5)<0 Теперь вынесем за скобки общий множитель (х-5), получим: (х−5)(х−5−√7)<0 Найдем нули функции, приравнивая каждый множитель к […]
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так […]
8х – х2≥0 Вынесем -х за скобки: -х(-8 + х) ≥0 Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 8) ≤0 Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8. Итак, имеем нули функции 0 и 8. Теперь расставляем их на числовом […]
Определение Методом интервалов решают неравенства вида: (х – х1)(х – х2)….(х – хn)>0 или (х – х1)(х – х2)….(х – хn)<0, где х1, х2, …, хn – не равные друг другу числа, х – переменная. Также в неравенствах могут быть использованы знаки ≤ или ≥. Данный вид записи неравенства будем называть – стандартный. Для решения […]
Определение Неравенство вида ax2+bx+c>0 или ax2+bx+c<0, где х – переменная, a, b и c некоторые числа называют неравенством второй степени с одной переменной (или квадратными неравенствами). Также в неравенствах могут встречаться знаки ≤ или ≥. Для решения неравенства находят промежутки, в которых функция у=ax2+bx+c принимает положительные или отрицательные значения, это зависит от знака неравенства, данного […]
Определение Выражение с одной переменной, содержащее знак неравенства, называется неравенством с одной переменной. Например: 23х+11<11x+5; 6x–10; х>9 Неравенства такого вида называют линейными неравенствами с одной переменной, так как х в них в первой степени. Вспомним, что в зависимости от знака неравенства, их называют строгие знаки (< и >) или нестрогие знаки (≤ и ≥). Решением […]
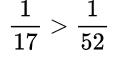
Определение Числовое неравенство – это неравенство, в котором по обе стороны от знака неравенства содержатся числа или числовые выражения. Результат сравнения записывают с помощью знаков =, <, >. Например, 24=24; 46>13, 67<21, –15>–65. В зависимости от конкретных чисел используется способ сравнения, но существует способ, который охватывает все числа, он основывается на следующем определении. Способ сравнения […]