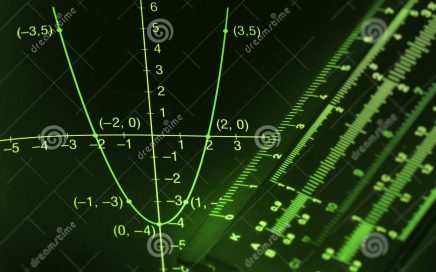
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении). Теперь поработаем с графиками и подпишем на […]
Теория к заданию №11 Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы. На произвольном примере ознакомимся с исследованием функции: область определения и множество значений корни и критические точки промежутки возрастания убывания Теперь рассмотрим данный материал на линейной функции: y = kx + b где k – […]
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3. У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. […]
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось […]
Для решения данной задачи необходимо знать вид графиков функций, а именно: y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1 x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b […]
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида: y = kx + b График данной функции зависит от k и b. если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках […]
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой. Общие правила: если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти […]
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида y = ax² + bx + c Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз. Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0. У первой и третьей ветви […]