Значения функции: наибольшее и наименьшее
В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.
Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=»#defae6″]
Найти точку максимума функции y = ln(x+4)2+2x+7.
[/su_note]
Алгоритм решения:
- Определяем область определения функции.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие области определения.
- Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
- Записываем ответ.
Решение:
1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:
(x+4)2 > 0
Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.
2. Находим производную:
у’=(ln(x+4)2 + 2x + 7)’
По свойству логарифма получаем:
у’=(ln(x+4)2 )’+(2x)’+(7)’.
По формуле производной сложной функции:
(lnf)’=(1/f)∙f’. У нас f=(x+4)2
у, = (ln(x+4)2 )’+ 2 + 0 = (1/(x+4)2 )∙((x+4)2)’ + 2=(1/(x+4)2 2)∙(х2 + 8х + 16)’ +2=2(х + 4) /((х + 4)2) + 2
у’= 2/(х + 4) + 2
3. Приравниваем производную к нулю:
у, = 0 → (2+2∙(х + 4))/(х + 4)=0,
2 +2х +8 =0, 2х + 10 = 0,
2х = -10,
х = -5
Ответ: -5.
Второй вариант задания (из Ященко, №1)
[su_note note_color=»#defae6″]
Найдите точку минимума функции y = x – ln(x+6) + 3.
[/su_note]
Алгоритм решения:
- Определяем область определения функции.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие области определения.
- Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
- Записываем ответ.
Решение:
1. ОДЗ: ![]() .
.
2. Найдем производную функции:
![]()
3. Приравниваем полученное выражение к нулю:
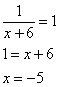
4. Получили одну точку x=-5, принадлежащую области определения функции.
5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4
![]()
При х=-5,5 производная функции отрицательна, так как
![]()
Значит, точка х=-5 является точкой минимума.
Ответ: -5.
Третий вариант задания (из Ященко, №12)
[su_note note_color=»#defae6″]
Найдите наибольшее значение функции ![]() на отрезке [-3; 1].
на отрезке [-3; 1].
[/su_note]
Алгоритм решения:.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие заданному отрезку.
- Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
- Находим значения функции на концах отрезка.
- Ищем среди полученных значений наибольшее.
- Записываем ответ.
Решение:
1. Вычисляем производную от функции, получим
![]()
2. Приравниваем производную к нулю:
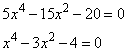
Решение уравнения дает два корня
![]() — не принадлежит множеству действительных чисел
— не принадлежит множеству действительных чисел
![]() .
.
3. Значение ![]() и остается одна точка
и остается одна точка ![]() .
.
4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:
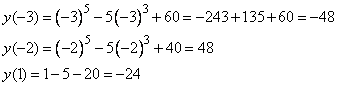
Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.
Ответ: 48.