Задание №16 ЕГЭ по математике профильного уровня

---

Планиметрия

---

В 16 задании профильного уровня ЕГЭ по математике — задача геометрическая, а именно планиметрическая. Уровень сложности высокий по шкале ЕГЭ и школьной геометрии, поэтому приступать к этому заданию необходимо с хорошей подготовкой. Я рекомендую приступать к задаче тем, кто более чем на 5 знает геометрию. Итак, приступим к рассмотрению одного из вариантов.

---

Разбор типовых вариантов заданий №16 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=»#defae6″]

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

[/su_note]

Алгоритм решения:

а)

1. Выполняем рисунок.
2. Используем свойство касательной для определения вида треугольника
3. Показываем, что AD  и  BC  параллельны.

б)

1. Вводим определенность относительно радиусов окружностей. И доказываем подобие треугольников ВКС и АКD.
2. Определяем отношение площадей.
3. Определяем искомую площадь.

Решение:

а) 1. Выполняем рисунок, учитывая условие задачи.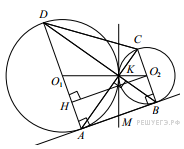

Пусть О₁ и О₂ центры данных окружностей, а М – точка пересечения общей касательной и касательной, проведенной в к окружностям в точке К.

2. По свойству касательных, проведённых из одной точки,  AM=KM  и.  KM=BN.  Треугольник  у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.

3. Вписанный угол  ∠AKD  прямой, поэтому он опирается на диаметр AD  Значит,  AD⊥AB.  Аналогично получаем, что  BC⊥AB  Следовательно, прямые  AD  и  BC  параллельны. б) 1. Пусть радиус первой окружности равен 4, тогда радиус второй 1. Рассмотрим треугольники  BKC  и  AKD .  и общий угол. По признаку подобия. Эти треугольники подобны. Пусть  , тогда  2. У треугольников AKD и AKB общая высота, следовательно,   то есть  Аналогично,   Площадь трапеции  ABCD  равна  25S Вычисляем площадь трапеции  ABCD  Для этого опускаем на  AD  перпендикуляр  O2H Его длина равна высоте трапеции. Определяем его из треугольника  O2HO1 по теореме Пифагора: 3. Отсюда   Имеем:  25S=20  откуда  S=0,8   Ответ: 3,2.

---

Второй вариант (Из Ященко,№1)

[su_note note_color=»#defae6″]

В трапеции ABCD основание AD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.

а) Докажите, что ВМ = СМ.

б) Найдите угол ЛВС, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.

[/su_note]

Алгоритм решения:

а)

1. Выполняем рисунок, исходя из условия.
2. Устанавливаем соотношения между величинами.
3. Делаем вывод

б)

1. Проводим перпендикуляр к стороне ВС.
2. Устанавливаем необходимые соответствия.
3. Определяем искомую величину угла.

Решение:

а) 1. Выполняем рисунок, исходя из условия.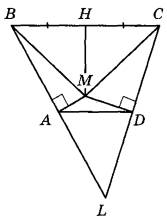

2. Прямые АВ и CD по условию пересекаются. Обозначим точку их пересечения буквой L. Тогда треугольник BLC подобен ALD, причем, коэффициент подобия равен 2, потому как ВС = 2AD. Значит, А и D являются серединами сторон BL и CL соответственно.

Тогда AM и DM — серединные перпендикуляры к сторонам треугольника BLC. Из этого вытекает, что М — центр окружности, описанной около него окружности.

3. Значит, BM = CM как радиусы этой окружности б)

1. Пусть Н — середина ВС, тогда МН является серединным перпендикуляром к ВС. Тогда треугольники ВНМ и СНМ являются равнобедренными и прямоугольными. Потому ∠BCM=90° .

2. По свойству вписанного угла , Отсюда искомый угол Ответ: 71⁰.