Задание №18 ЕГЭ по математике профильного уровня

---

Задачи с параметром

---

В 18 задании —  предпоследнем задании профильного уровня ЕГЭ по математике — необходимо продемонстрировать умение решать задачи с параметрами. В подавляющем большинстве данное задание представляет собой систему из двух уравнений с параметром а, и необходимо найти такие значения, при которых система будет вести себя заданным образом — иметь два или одно или вообще не иметь решений.

---

Разбор типовых вариантов заданий №18 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=»#defae6″]

Найдите все положительные значения a, при каждом из которых система имеет единственное решение:

• (|x|–5)²+(y–4)²=4
• (x–2)²+y²=a²

[/su_note]

Алгоритм решения:

1. Рассматриваем второе уравнения, устанавливаем, что является его графиком.
2. Определяем условие единственности решения.
3. Находим расстояние между центрами, определяем значения параметра.
4. Записываем ответ.

Решение:

1. Первое уравнение — это две окружности радиусами 3 и координатами центров С ₂(5;4) и С₂(-5;4). Одну окружность задает данное уравнение при х≥0, а вторую – при х<0. Они не пересекаются и не касаются.

2. Второе уравнение — это одна окружность радиуса «а» с координатами центра: С (-2;0).

3. Наличие единственного решения означает, что одна окружность должна коснуться одной из окружностей в одной точке. Поэтому следует решить попарно две системы.

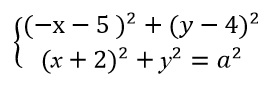
Первая: Вторая:

Естественно, в первом и втором случае получается пара корней т. е. координат касания внешним и внутренним образом.

Но стоит заметить что нас будут интересовать только корни определяющие касание внешнее левой окружности и касание внутреннее правой окружности. Т. к. два других уравнения противоречить условию и будут иметь более одного решения. Достаточно взглянуть на прилагаемый рисунок:

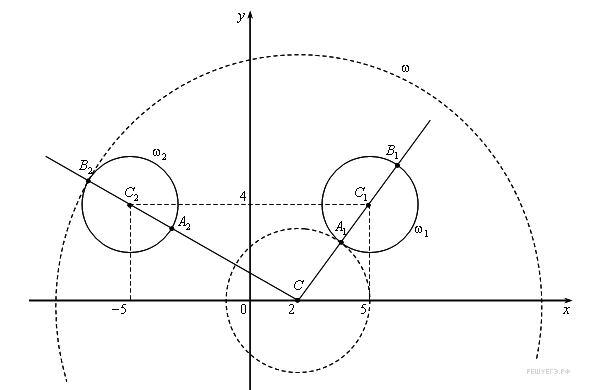
4. Воспользуемся приложенным рисунком. Проведем лучи СС₁, и СС₂, обозначив точки их пересечения с окружностями А₁, В₁ и А₂, В₂. Тогда

Если a<CA2 или CA2<a<CB2 окружности не пересекаются. А это означает, корней система иметь не может.

5. Имеем: исходная система имеет единственное решение при

Ответ:

---

Второй вариант (из Ященко, №1)

[su_note note_color=»#defae6″] Найдите все значения а, при каждом из которых уравнение имеет ровно один корень. [/su_note]

Решение:

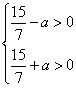
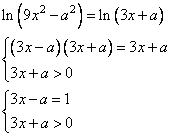
Данное уравнение равносильно виду: Рассматриваем случай:  при условии Получаем . При этом значении х условие принимает вид: Отсюда Имеем в данном случае:  при . Рассмотрим теперь случай: , при этом . Решаем уравнение. Получаем: Отсюда . Условие принимает вид: Следовательно, получается . То есть  при . Корни  и  равны между собой, если . Таким образом, уравнение имеет только один корень если  и . Ответ: