Задание №2 ОГЭ по физике

Кинематика. Силы в природе.

Для решения задания № 2 необходимо понимание процессов, связанных с механических движением тел. Требуется знание физических понятий, величин и явлений, изучаемых в курсе кинематики и динамики. Это, в частности, понятия перемещения, скорости, ускорения, а также сил, действующих на объекты в макромире. Необходимая для решения информация содержится в разделе теории.

Теория к заданию №2 ОГЭ по физике

Скорость и ускорение при равномерном и равнопеременном движении

Задание №2 ОГЭ по физикеПри равномерном (прямолинейном) движении скорость   есть величина постоянная ( ), поскольку за каждую единицу времени тело проходит одинаковые расстояния. По причине того, что скорость со временем не изменяется, ускорение  при равномерном движении отсутствует, т.е.  .

Равнопеременное движение бывает 2 видов – равноускоренное и равнозамедленное. При равноускоренном движении скорость в каждую единицу времени увеличивается на одинаковую величину и, соответственно,  . Вектор ускорения при этом сонаправлен с вектором скорости (  ) При равнозамедленном движении происходит обратный процесс: скорость в каждую единицу времени уменьшается на одну и ту же величину и поэтому  . Вектор ускорения в этом случае имеет направление, противоположное вектору скорости (  ).

Хорошо иллюстрирует разные виды движения такой график:

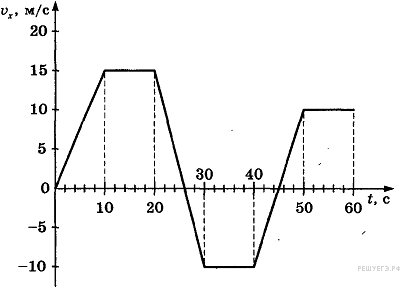
Здесь в течение 0-10 с и 40-50 с тело двигалось равноускоренно, в течение 20-30 с – равнозамедленно. Чтобы найти из графика ускорение на заданном промежутка, достаточно взять любую точку на соответствующем участке графике и опустить из нее перпендикуляры на оси. Полученные значения, а также данные в точке начала промежутка, следует использовать для расчета по формуле для ускорения:  .

Пример расчета. Рассмотрим 3-й промежуток (20-30с). Возьмем точку с координатами (26; 0), для которой  . Получаем:  , что означает, что тело двигалось с ускорением, равным 2,5 м/с2, а знак минус указывает на то, что движение было равнозамедленным.

На промежутках 10-20 с, 30-40 с и 50-60 с движение было равномерным (а=0).

Неравномерное движение

При неравномерном движении скорость не может быть найдена из единственной формулы, поскольку ее значения в разные промежутки времени произвольно отличаются, не подчиняясь общему закону. В этом случае говорят о мгновенной скорости в каждый момент времени и ее среднем значении на данном участке пути. Средняя скорость при этом определяется как  . Если нужно найти среднюю скорость на нескольких последовательных участках пути, то ищут среднее арифметическое скоростей на каждом из участков:  .

Координаты материальной точки

В соответствии с ОЗМ координаты матер.точки позволяют определить ее положение в пространстве в заданной с-ме координат относительно выбранного тела отсчета в произвольный момент времени. Для каждой материальной точки может быть определено от 1 до 3 координаты в зависимости от количества осей выбранной с-мы координат – x, y, z.

В самом общем случае координата тела может быть найдена по формуле:

 ,

где  – начальная координата, т.е. расстояние точки от начала отсчета в начальный момент времени ее движения;  – проекция перемещения, совершенного точкой за заданный промежуток времени, на ось Х.

Координаты y и z определяются аналогично.

При равномерном перемещении координаты определяются так:

,

,

,

где  ,  ,  – проекции вектора скорости на соответствующие координатные оси.

При равноускоренном перемещении координаты находятся по формулам:

,

 ,

,

где , , – проекции вектора начальной скорости на соответствующие оси; , , – проекции вектора ускорения на соответствующие оси.

Те же формулы, но без учета начальных значений , и позволяют определить пройденный телом путь.

Инерциальная система отсчета

Система отсчета, в которой (относительно которой) физ.тело движется с постоянной скоростью (т.е. без ускорения) или находится в покое, называется инерциальной. Типичный пример – человек, сидящий в салоне транспорта. В этом случае он находится в инерциальной системе, связанной с этим транспортом, и пребывает в ней в покое вне зависимости от того, с каким ускорением транспорт движется относительно объектов за его пределами.

Соответственно, тело находится в неинерциальной с-ме отсчета, если оно движется с ускорением относительно объекта, в связке с которым рассматривается.

Закон всемирного тяготения

Модуль (величина) силы, с которой тела притягиваются, пропорционален произведению масс этих тел и обратно пропорционален квадрату расстояния между ними. Формула закона:

 ,

где m1 и m2 – массы соответственно 1-го и 2-го тел, R – расстояние между телами.

G – гравитационная постоянная. Это константа (постоянная величина), ее значение составляет  .

З-н всемирного тяготения используется в первую очередь для определения величины взаимодействия между Землей и объектам вне ее пределов, с другими планетами, а также взаимодействия космических объектов между собой. В случае если объект, взаимодействующий с Землей находится близко от нее, то для R используется расстояние не от поверхности Земли, а от ее центра.

Силы в природе

Сила тяжести. Эта сила действует на всякий материальный объект, находящийся на поверхности Земли или над нею, но в поле ее тяготения. Именно сила тяжести обеспечивает падение (притяжение) тел на Землю. Сила тяжести вычисляется по формуле  , где ɡ – ускорение свободного падения. ɡ – константа, равная:  . Вектор FT, равно как и вектор ɡ, всегда направлен вертикально вниз, т.е. перпендикулярно к поверхности земли.

Сила реакции опоры. Это сила, с которой на тело действует твердое основание, на котором оно находится. Она обусловлена 3-м законом Ньютона и возникает как противодействие силе тяжести. Когда тело покоится на горизонтальной поверхности, то реакция опоры и сила тяжести равны. Обозначается реакция опоры обычно как  .

Сила трения. Она возникает при соприкосновении (контакте) физ.тел и направлена вдоль поверхности контакта всегда противоположно возможному или реальному направлению движения тела. Различают трение покоя и скольжения. Трение покоя не приводит к реальному движению тела, скольжение – приводит. Вычисляет сила трения по формуле:  , где μ – коэффициент трения. Из формулы видно, что сила трения пропорциональна реакции опоры, т.е. силе нормального давления, прикладываемого к телу.

Сила упругости. Она возникает при сжатии или растяжении тела и выражается в сопротивлении этому процессу. Вычисляют силу упругости по з-ну Гука:  , где х – величина удлинения или сжатия (деформации), k – жесткость. Знак «–» указывает, что сила упругости всегда направлена противоположно направлению деформации.

Колебательные движения: основные понятия

Амплитудой называют максимальное значение колеблющейся физ.величины в процессе колебаний. Т.е. амплитуда – это максимальное отклонение от состояния равновесия.

Период колебания – это наименьший временной промежуток, за который происходит возврат всех параметров колебательного процесса к исходному значению. Т.е. период колебаний – это время, по истечении которого все параметры колебательного движения повторяются. За 1 период осуществляется 1 полное колебание.

Частота колебаний представляет собой количество полных колебаний за единицу времени. Отсюда следует, что частота – величина, обратная периоду.

Высота тона – субъективная характеристика колебательного движения, поскольку ее восприятие человеческим ухом может отличаться у разных людей и у живых существ в целом. Высота тона непосредственно связана с частотой, а именно: высота тона пропорциональна частоте. Это означает, что чем больше колебательных движений происходит в единицу времени, тем больше высота тона, и наоборот.

Разбор типовых вариантов заданий №2 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

На рисунке представлены графики зависимости изменения давления воздуха p от времени t для звуковых волн, издаваемых двумя камертонами. Сравните амплитуду изменения давления и высоту тона волн.

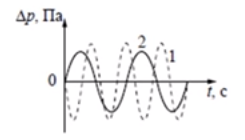
  1. Амплитуда изменения давления одинакова; высота тона первого звука больше, чем второго.
  2. Высота тона одинакова; амплитуда изменения давления в первой волне меньше, чем во второй.
  3. Амплитуда изменения давления и высота тона одинаковы.
  4. Амплитуда изменения давления и высота тона различны.

[/su_note]

Алгоритм решения:
  1. Анализируем приведенный в условии график. Сравниваем амплитуды камертонов, делаем соответствующий вывод.
  2. Сравниваем высоту тона камертонов.
  3. Анализируем предложенные варианты ответов. Определяем номер правильного.
  4. Записываем ответ.
Решение:
  1. Из рисунка видно, что колебания 1-го камертона обозначены пунктирной линией, 2-го – сплошной. При этом рисунок демонстрирует, что линия пунктирного графика даст большую проекцию на ось ординат (∆р). Это означает: амплитуда изменения давления 1-го камертона больше амплитуды 2-го.
  2. Поскольку высота тона пропорциональна частоте, то условно можно утверждать, что она дублирует частоту. В свою очередь частота напрямую связана с периодом. Из рисунка видно, что период колебаний 1-го камертона (красная линия) меньше, чем период 2-го (синяя линия):

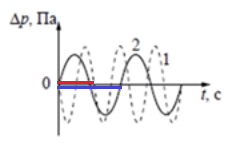
Это значит, что с частотой дело будет обстоять с точностью до наоборот, т.е. у 1-го камертона частота больше, чем у 2-го. Соответственно, можем утверждать, что высота тона 1-го камертона больше, чем у 2-го.

Проанализируем варианты ответов. Ответ 1 неверен в первой своей части. Ответ 2 неверен в обеих частях утверждения. Ответ 3 неверен, т.к. доказано, что обе величины различны. Таким образом, правильный вариант ответа – 4.

Ответ: 4

Первый вариант (Камзеева, № 2)

[su_note note_color=»#defae6″]

С летящего самолета (рис. 1) через грузовой люк сбрасывают груз. Какое направление соответствует направлению ускорения груза сразу после его сбрасывания (рис. 2)? Сопротивлением воздуха пренебречь.

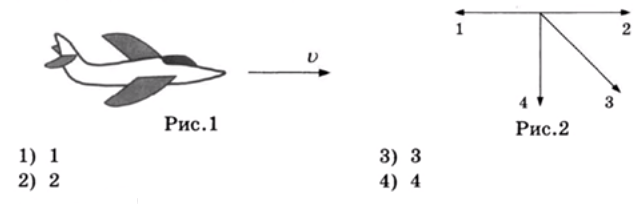
[/su_note]

Алгоритм решения:
  1. Определяем воздействие на груз и его параметры в горизонтальной плоскости. Определяем ускорение груза в горизонтальной плоскости.
  2. Выполняем аналогичный анализ для вертикальной плоскости.
  3. Делаем вывод относительно правильного варианта ответа.
  4. Записываем ответ.
Решение:
  1. Поскольку сопротивлением воздуха в условии предлагается пренебречь, то в горизонтальной плоскости в момент сбрасывания груза он движется в инерциальной с-ме отсчета, связанной с самолетом, со скоростью v (см. рис. 1). Ускорение при этом равно нулю, т.е. горизонтальная составляющая (проекция) вектора ускорения отсутствует.
  2. В вертикальной плоскости в момент отделения груза от самолета на него начинает действовать сила тяжести. Других внешних сил нет. Соответственно, груз приобретает ускорение g (свободного падения), которое направлено вертикально вниз. Это означает, что у груза имеется вертикальная составляющая (проекция) ускорения.
  3. Таким образом, вектор ускорения груза в момент его сбрасывания направлен вертикально вниз, и правильный вариант ответа – 4.

Ответ: 4

Второй вариант (Камзеева, № 5)

[su_note note_color=»#defae6″]

Искусственный спутник Земли движется по круговой орбите на высоте h от поверхности Земли (см. рис.).

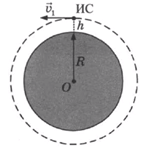
Как изменится сила притяжения спутника к Земли при уменьшении высоты в 2 раза?

  1. увеличится в 2 раза
  2. увеличится в 4 раза
  3. увеличится менее чем в 4 раза
  4. увеличится более чем в 4 раза

[/su_note]

Алгоритм решения:
  1. Записываем уравнение з-на всемирного тяготения (для F).
  2. Записываем уравнение закона для ситуации, когда высота спутника уменьшилась в 2 раза (для F1).
  3. Находим отношение F1 к F.
  4. Определяем верный вариант ответа.
  5. Записываем ответ.
Решение:
  1. Согласно закону всемирного тяготения 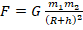 . В качестве расстояния между телами используем расстояния от центра Земли до спутника.
  2. Если высота h уменьшилась в 2 раза, то расстояние стало равным 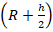 . Поэтому  .
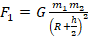  3. Очевидно, что при определении отношения F1 и F массы тел и G сократятся (поскольку они не меняются), а расстояния распределятся так: расстояние в формуле для F окажется в числителе отношения, а расстояние в формуле для F1 – в знаменателе. Т.е. получаем: .
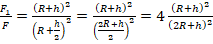  4. Анализируем предложенные варианты ответов. Правильность ответа 1 невозможно определить, потому что неизвестны точные значения для R и h. Ответ 2 неверен, поскольку в 4 раза расстояние увеличилось бы только в ситуации, если бы в знаменателе при R не было 2, а так расстояние уменьшается меньше, чем в 4 раза (с двойкой знаменатель больше числителя и общее отношение меньше 1). Этот же анализ указывает на неправильность и ответа 4. А вот ответ 3 в соответствии с ним полностью верен.

Ответ: 3

Текст: Базанов Даниил, 11.1k 👀