Задание №26 ОГЭ по физике

Расчетная задача (механика, термодинамика, электродинамика, магнитные явления)

Задание №26 ОГЭ по физике имеет комплексный характер, потому что может охватывать до 3-х разделов курса. В задании могут сочетаться, к примеру, элементы электродинамики, термодинамики и использоваться одно-два перекликающихся с ними физ.понятия из механики. Для решения задания требуется достаточно глубокое понимание происходящих физ.процессов, чтобы корректно ввести нужные формулы, грамотно сочетать их между собой и произвести результирующие расчеты. Необходимые теоретические сведения рекомендуется искать в разделах теории соответствующих по темам заданий из 1-й части ОГЭ.

Разбор типовых вариантов заданий №26 ОГЭ по физике

Демонстрационный вариант 2019

[su_note note_color=»#defae6″]

Кусок свинца, имеющего температуру 27 °С, начинают нагревать на плитке постоянной мощности. Через 10 минут от начала нагревания свинец нагрелся до температуры плавления. Сколько ещё времени потребуется для плавления свинца?

[/su_note]

Алгоритм решения:
  1. Записываем краткое условие.
  2. Записываем ф-лы для мощности при нагревании и плавлении свинца. Объединяем их и выражаем темп-ру плавления (1).
  3. Определяем ф-лы (2) и (3) для расчета кол-ва теплоты, поглощаемой свинцом при нагревании и плавлении.
  4. Подставляем (2) и (3) в (1). Вычисляем темп-ру плавления. Записываем ответ.
Решение:
  1. Дано: t=27 0C, τ=10 мин, tпл=327 0С, τпл – ?
  1. Расчетная ф-ла в данном случае будет выглядеть как отношение кол-ва теплоты ко времени. Поэтому при нагревании 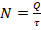, а при плавлении 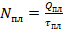. Поскольку по условию мощность плитки N=const, то N=Nпл и 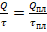. Отсюда выразим время плавления: .
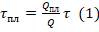  2. При нагревании до темп-ры плавления свинец поглотит кол-во теплоты, равное: Q=cm(tпл–t) (2). При плавлении кол-во поглощенной теплоты составит: Qпл=λm (3). С=Здесь с – уд.теплоемкость свинца, λ – уд.теплота его плавления (табличные величины). с=130 дж/(кг·0С), λ=2,5·104 Дж/кг.
  3. (2, 3 → 1): 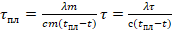. Вычислим темп-ру плавления: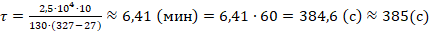

Ответ: ≈385 с

Первый вариант (Камзеева, № 3)

[su_note note_color=»#defae6″]

Определите массу никелированной проволоки площадью поперечного сечения 1 мм2, из которой изготовлен реостат, если при напряжении на его концах 24 В сила протекающего тока равна 3 А. Плотность никелина принять равной 8800 кг/м3.

[/su_note]

Алгоритм решения:
  1. Составляем краткое условие.
  2. Записываем ур-ние для искомой массы. Выражаем объем проволоки через ее длину и попер.сечение. Корректируем соответственно ур-ние для массы (1).
  3. Записываем ф-лу для сопротивления из з-на Ома для участка цепи. Фиксируем ф-лу для сопротивления через уд.сопротивление. Приравниваем эти ф-лы, выражаем длину проволоки (2).
  4. Подставляем (2) в (1), выводим рабочую ф-лу для вычисления массы.
  5. Вычисляем массу. Записываем ответ.
Решение:
  1. Дано: S=1 мм2 (1·(10-3)2=10-6 м2), U= 24 В, I=3 А, ρпл=8800 кг/м3, m – ?
  1. Искомую массу выразим через плотность и объем: m=ρпл·V. Поскольку по условию дан цилиндрический проводник (проволока имеет форму полнотелой трубки), то V=lS, где l – длина проводника, S – площадь его попер.сечения. Тогда m=ρплlS (1).
  2. На основании з-на Ома для участка цепи 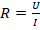. С другой стороны сопротивление можно выразить так: 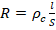, где ρс – уд.сопротивление проводника, которое является табличной величиной и равно ρс=0,4 Ом·мм2/м. Приравняем эти ф-лы: 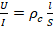. Отсюда выразим l: .
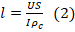  3. (2) → (1): 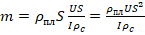. В этой формуле нужно учесть одну особенность. В ней присутствует: 1) плотность никелина, в которой фигурирует объем в ед.СИ, т.е. в м3 и, соответственно, площадь попер.сечения в м2; 2) уд.сопротивление, в ед.измерения которого присутствует мм2. Это означает, что в рабочей формуле, подставляя значение для S2, его следует взять 1 раз как положено в СИ (в м2), а 1 раз в мм2.
  4. Вычислим массу:

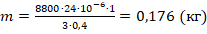
Ответ: 0,176 кг

Второй вариант (Камзеева, № 7)

[su_note note_color=»#defae6″]

Имеются два одинаковых электрических нагревателя. Если их соединить последовательно, то они нагревают 0,5 кг воды на 80 0С за 7 мин. Чему равна мощность одного нагревателя при включении в ту же электросеть? Потерями энергии пренебречь.

[/su_note]

Алгоритм решения:
  1. Составляем краткое условие.
  2. Записываем ф-лы для мощности 1 и 2 нагревателей через напряжение в электросети и сопротивление. Находим соотношение между этими мощностями.
  3. Записываем формулу для мощности 2 нагревателей, согласно определению этой физ.величины. Выражаем в ней работу через кол-во теплоты, поглощаемой водой.
  4. Определяем кол-во теплоты через уд.теплоемкость воды, ее массу и изменение темп-ры. Подставляем это ур-ние в ф-лу, содержащую отношение мощностей одного и двух нагревателей (см.п.2), получаем рабочую ф-лу для мощности 1 нагревателя.
  5. Вычисляем искомую мощность. Записываем ответ.
Решение:
  1. Дано: m=0,5 кг, ∆t=80 0С, τ=7 мин (7·60=420 c), Р1 – ?
  2. Если используется 1 нагреватель, то мощность 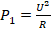. Если применяются 2 нагревателя, соединенные последовательно, то сопротивление становится равным 2R, а напряжение не меняется. Поэтому мощность составит 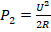. Из этих двух уравнений следует, что 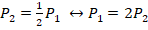, т.е. мощность 1 нагревателя в 2 раза выше, чем двух, соединенных последовательно.
  3. Запишем ф-лу для мощности, которая следует из определения этой физ.величины: P=A/τ. Причем работа в данном случае – это кол-во теплоты, которое передается воде от двух (по условию) нагревателей и поглощается нею для нагрева. Тогда мощность равна: P=Q/τ=Р2.
  4. Q определяется так: Q=cm∆t. Тогда P2=cm∆t/τ. Здесь с – уд.теплоемкость воды, которая составляет с=4200 Дж/(кг·0С) . Поскольку P1=2P2, то P1=2cm∆t/τ.
  5. Подсчитаем значение мощности: .

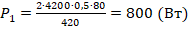Ответ: 800 Вт

Третий вариант (Камзеева, № 11)

[su_note note_color=»#defae6″]

Троллейбус движется равномерно прямолинейно со скоростью 36 км/ч. Сила тока в обмотке электродвигателя равна 40 А, напряжение равно 550 В. КПД электродвигателя равен 80%. Чему равен коэффициент трения? Масса троллейбуса 11 т.

[/su_note]

Алгоритм решения:
  1. Составляем краткое условие.
  2. Зарисовываем схему действующих на троллейбус сил. Записываем их векторное ур-ние, согласно 2-му з-ну Ньютона.
  3. Формируем ур-ние проекций сил на ось Ох. Выражаем из него ур-ние для силы тяги (1).
  4. Формируем ур-ние проекций на ось Оу. Из него получаем (2).
  5. Записываем ф-лу для силы трения. Используя (2), получаем ур-ние для силы трения через массу троллейбуса, т.е. избавляемся от величины норм.давления (3).
  6. Записываем ф-лу для КПД через работу. Выражаем полезную и затраченную работы через соответствующие ф-лы. Преобразуем с их помощью ф-лы для КПД так, чтобы в ней присутствовали только величины, данные в условии, и искомый коэф-т трения (4).
  7. Подставляем (3) в (4), выражаем искомую величину. Вычисляем коэф-т трения. Записываем ответ.
Решение:
  1. Дано: v=36 км/ч (36:3,6=10 м/с), I=40 А, U=550 В, ɳ=80%, m=11 т 11·103 кг, μ – ?
  2. На троллейбус действуют силы: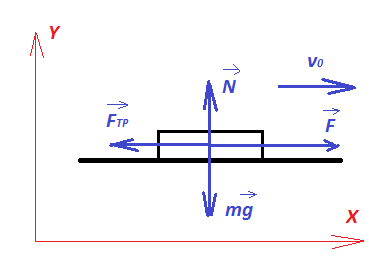По 2-му з-ну Ньютона 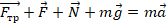, где F – сила тяги электродвигателя.
  3. В проекции на ось ОХ получим: F–Fтр=0. В правой части получен ноль, т.к. по условию движение равномерное, а значит, осуществляется без ускорения (или с нулевым ускорением). Отсюда: F=Fтр (1).
  4. В проекции на ось Оу имеем: N–mg=0. Отсюда: N=mg (2).
  5. Сила трения равна: Fтр=μN. Используя (2), получим: Fтр=μmg и, подставив эту ф-лу в (1), имеем: F=μmg (3).
  6. Запишем ф-лу для КПД: 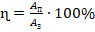. Полезная работа здесь – это работа силы тяги (F). Значит, AП=F·s, где s – перемещение троллейбуса. Затраченная работа представляет собой работу силы тока в электродвигателе. Тогда АЗ=UIt, где t – время протекания эл.тока. Следовательно, ф-ла для КПД приобретет вид: 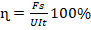. Поскольку движение по условию прямолинейное и равномерное, то s=vt. Отсюда: .
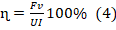  7. (3) → (4): 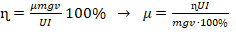. Вычислим μ: .

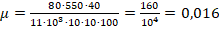Ответ: 0,016

Текст: Базанов Даниил, 2.2k 👀