Задание EF17578

▿повышенный уровень сложности▿ФИПИ(17578)

Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с². Чему равен радиус планеты? Ответ запишите в километрах.

📜Теория для решения: Гравитационные силы. Закон всемирного тяготения.

Посмотреть решение

Алгоритм решения

1.Записать исходные данные. Перевести единицы измерения в СИ.

2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.

3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.

4.Записать закон всемирного тяготения применительно к спутнику.

5.Вывести формулу для расчета радиуса планеты.

6.Подставить известные данные и произвести вычисление.

Решение

Запишем исходные данные:

• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙10³ м/с.

• Радиус орбиты спутника: R_о = 4000 км, или 4∙10⁶ м.

• Ускорение свободного падения у поверхности планеты: g = 4 м/с².

Ускорение свободного падения определяется формулой:

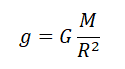
Отсюда радиус равен:

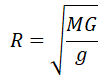
Линейная скорость и радиус орбиты связываются формулой:

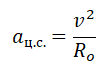
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:

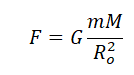
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:

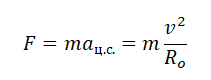
Отсюда:

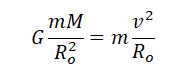
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:

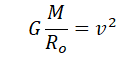
Из этой формулы выразим массу планеты:

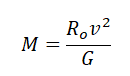
Подставим массу планеты в формулу для нахождения ее радиуса:

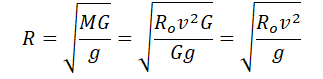
Подставляем известные данные и вычисляем:

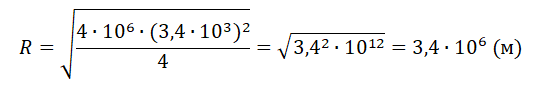
Этот радиус соответствует 3400 км.

Ответ: 3400

Текст: Алиса Никитина, 4k 👀

Подписаться

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии