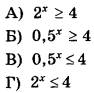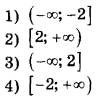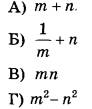Задание №17 ЕГЭ по математике базового уровня

---

Неравенства и сравнения

---

В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.

---

Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня

---

Вариант 17МБ1

[su_note note_color=»#defae6″]

На координатной прямой отмечены точки A, B, C и D.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

ТОЧКИ А В С D

ЧИСЛА 1) log2 10 2) 7/3 3) √26 4) (3/5)-1

[/su_note]

Алгоритм выполнения:

1. Проанализировать рядом с каким из целых чисел стоит данная точка.
2. Проанализировать на каком интервале лежат числа из правого столбца.
3. Сравнить полученные интервалы и поставить в соответствие.

Решение:

1. Рассмотрим точку А. Ее значение больше 1 и меньше 2.
2. Рассмотрим точку B. Ее значение больше 2 и меньше 3.
3. Рассмотрим точку С. Ее значение больше 3 и меньше 4.
4. Рассмотрим точку D. Ее значение больше 5 и меньше 6.
5. Вспомним что такое логарифм.

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение: log_a x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.

В нашем случае а = 2, x = 10.

То есть нас интересует число 2^b = 10. 2³ = 8 и 2⁴ = 16, следовательно, b лежит в промежутке от 3 до 4.

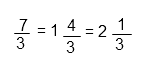
Следовательно, 7/3 больше 2 и меньше 3.

Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.

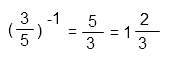
То есть (3/5)^-1 больше 1 и меньше 2.

Поставим в соответствие полученные интервалы.

А — (3/5)^-1 — 4

В — 7/3 – 2

С — log₂ 10 – 1

D — √26 – 3

Ответ: 4213.

---

Вариант 17МБ2

[su_note note_color=»#defae6″]

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА

РЕШЕНИЯ

[/su_note]

Алгоритм выполнения:

1. Представить правые и левые части неравенств в виде степени одного и того же числа.
2. Сравнить степени, так как основания равны.
3. Поставить в соответствие предложенные интервалы.

Решение:

А)

Представим 4 в виде степени с основанием 2. 2² = 4.

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

то есть,   — вариант под номером 2.

Б)

Число 0,5 можно представить как  , значит (0,5)^x = (2^-1) ^x = 2^-x

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.

то есть,   — вариант под номером 1.

В)

Аналогично с вариантом Б.

Число 0,5 можно представить как  , значит (0,5)^x = (2^-1) ^x = 2^-x

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.

то есть,   — вариант под номером 4.

Г)

Представим 4 в виде степени с основанием 2. 2² = 4.

Неравенство примет вид:

Основания степеней одинаковы, следовательно, степени соотносятся так же.

и   — вариант под номером 3.

Ответ: 2143.

---

Вариант 17МБ3

[su_note note_color=»#defae6″]

На прямой отмечены числа m и n.

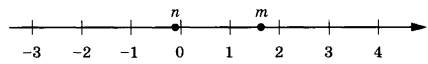
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

ЧИСЛА

ОТРЕЗКИ

[/su_note]

Алгоритм выполнения:

1. Найти промежутки в которых лежат числа m и n.
2. Оценить интервалы, в которых лежат выражения в левом столбце.
3. Поставить им в соответствие интервалы из правого столбца.

Решение:

Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3.

Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2.

Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1.

Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4.

Ответ: 3214.

---

Вариант 17МБ4

[su_note note_color=»#defae6″]

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

[/su_note]

Рассмотрим первое неравенство:

2^x≥4

представим 4 как 2², тогда:

2^x ≥ 2²

x ≥ 2

Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2^-1:

2^-x ≥ 4

2^-x ≥ 2²

-x ≥ 2

x≤-2

Ответ: А-4, Б-3, В-2, А-1.

---

Вариант 17МБ5

[su_note note_color=»#defae6″]

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

[/su_note]

Алгоритм выполнения

1. Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
2. Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».

Решение:

А. 2^–х+1 < 0,5 → 2^–x+1 < 2^–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.

Б.

Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.

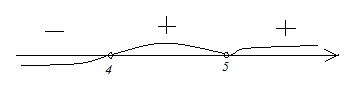
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).

Соответственно, имеем: Б–4.

В. log₄x > 1 → log₄x > log₄4 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.

Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.

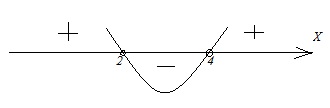
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).

Ответ: Г–2.

---

Вариант 17МБ6

[su_note note_color=»#defae6″]

На координатной прямой отмечены точки А, В, С и D.

Число m равно √2.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

[/su_note]

Алгоритм выполнения

Для каждого из выражений правого столбца делаем следующее:

1. Подставляем вместо m его числовое значение (√2). Вычисляем приблизительное значение.
2. Ориентируясь на целую часть полученного числа, находим соответствующее значение на координатной прямой.
3. Фиксируем пару «буква–число».

Решение:

1. 

Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.

1. 

Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.

1. 

Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.

1. 

Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.

---

Вариант 17МБ7

[su_note note_color=»#defae6″]

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

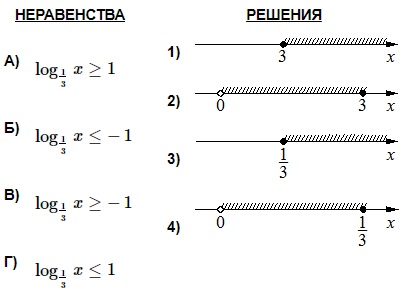
[/su_note]

Алгоритм выполнения

1. Последовательно решаем каждое неравенство (А–Г), получая в ответе промежуток значений. Находим соответствующее ему графическое отображение в правой колонке (Решения).
2. При решении неравенств учитываем, что: 1) при снятии знаков логарифма с основанием, меньшим 1, знак неравенства меняется на противоположный; 2) выражение под знаком логарифма всегда больше 0.

Решение:

А.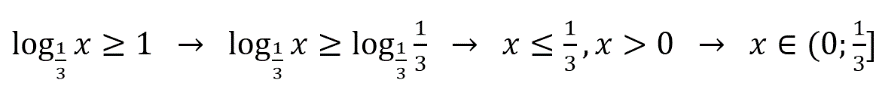

Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.

Б.

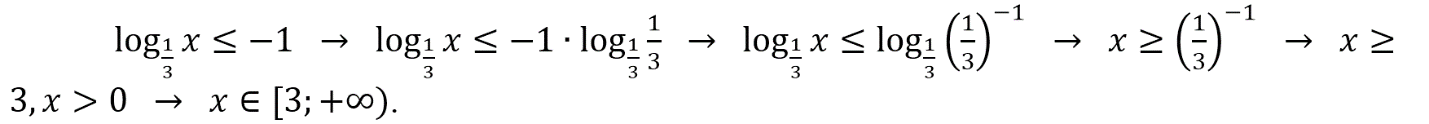
Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.

В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.

Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.

---

Вариант 17МБ8

[su_note note_color=»#defae6″]

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.

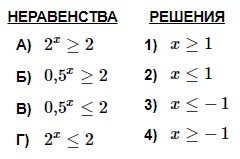
[/su_note]

Алгоритм выполнения

1. Решаем неравенство А. Находим номер соответствующего ответу решения из правой колонки.
2. Рассматриваем неравенство Г как подобное неравенству А. Определяем для него номер решения из правого столбца.
3. Решаем неравенство Б, перейдя к основанию 2. Определяем соответствующий для него номер варианта решения.
4. По аналогии с неравенством Б решаем неравенство В.

Решение:

А. 2^х ≥ 2 → 2^х ≥ 2¹ → х ≥ 1. Имеем: А–1.

Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.

Б. 0,5^х ≥ 2 → (1/2)^х ≥ 2 →2^–х ≥ 2¹ х ≤ –1. Имеем: Б–3.

В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.

---

Вариант 17МБ9

[su_note note_color=»#defae6″]

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

[/su_note]

Алгоритм выполнения

1. Подобные неравенства решаются методом интервалов. На координатной прямой отмечаются точки, являющиеся корнями соответствующего кв.ур-ния; промежутки между этими точками имеют определенные знаки, причем 1-й из них справа (от +∞ до самого большого корня) всегда имеет знак «+». Далее, продвигаясь справа налево, знаки чередуем, т.е. 2-й справа промежуток будет иметь знак «–», 3-й – «+» и т.д.
2. Если в неравенстве имеется выражение вида (х–а)², то знак промежутка при прохождении точки а не меняется.
3. Поскольку все неравенства строгие, то точки-корни в промежутки для ответов не включаются, что в результате фиксируется посредством круглых скобок.
4. Знак «ᴗ» является объединяющим и должен прочитываться как «или».

Решение:

Корнями в этих неравенствах являются х=1 и х=4.

Для неравенства А на прямой имеем:

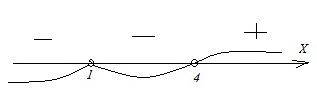
Результатом здесь будут промежутки с отрицательным знаком, т.е. х < 1 или 1 < x < 4. Ответ: А–3.

Для неравенств Б и В получаем на прямой:

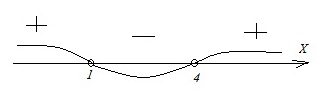
Для ответа в неравенстве Б следует взять промежутки со знаком «+». Получим: х < 1 или x > 4. Ответ: Б–1.

В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 < x < 4. Ответ: В–4.

Б. Отмечаем на прямой корни и промежутки с соответствующими знаками:

Для неравенства Г на прямой получили:

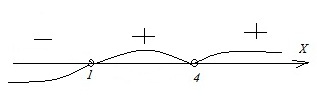
Результат – промежутки с положительным знаком. Тогда имеем: 1 < x < 4 или x > 4. Ответ: Г–2.

---

Вариант 17МБ10

[su_note note_color=»#defae6″]

На координатной прямой отмечены точки А, В, С и D.

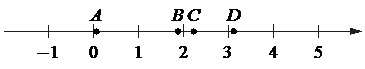
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

[/su_note]

Алгоритм выполнения

1. Определяем приблизительное значение чисел, приведенных в правом столбце, или их целую часть, что позволит выяснить, между какими двумя целыми числами на координатной прямой они располагаются.
2. Фиксируем пары «буква–число» для заполнения итоговой таблицы ответов.

Решение:

Число 1. log₅5=1, log₅25=log₅5²=2log₅5=2·1=2. Т.к. 5<20<25, то 1<log₅20<2. Значит, на координатной прямой число log₅20 отображено точкой В. Ответ: В–1.

Число 2. . Это означает, что число отображено на прямой точкой С. Ответ: С–2.

Число 3. √10 совсем немного больше, чем √9=3. Это число точно меньше 4, поскольку 4=√16. Соответственно, √10 на прямой расположен между 3 и 4 и отображен точкой D. Ответ: D–3.

Число 4. 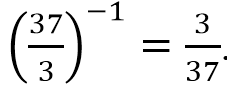Это положительная правильная дробь, а следовательно, она больше 0, но меньше 1. Тогда ей отвечает точка А. ответ: А–4.

---

Вариант 17МБ11

[su_note note_color=»#defae6″]

Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

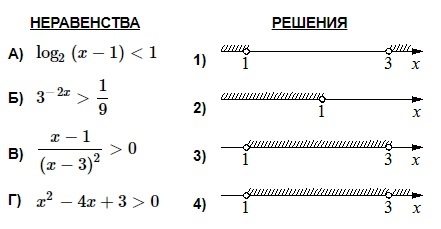
[/su_note]

Алгоритм выполнения

1. Решаем последовательно неравенства А–Г, учитывая ОДЗ.
2. По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.

Решение:

1. log₂ (x–1) < 1 → log₂ (x–1) < log₂ 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.

Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.

1. . ОДЗ не дает ограничений

Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.

1. Здесь не требуются преобразования. Решается неравенство методом интервалов. Точки пересечения с координатной прямой: х=1, х=3. Тогда имеем:

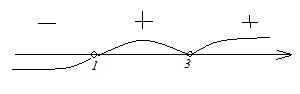
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.

1. х² – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:

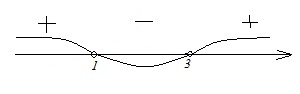
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.

---

Вариант 17МБ12

[su_note note_color=»#defae6″]

На координатной прямой отмечено число m.

Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

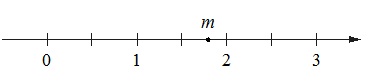
[/su_note]

Алгоритм выполнения

1. Определяем приблизительное значение для m.
2. Подставляем найденное значение для m последовательно в каждое из выражений (А–Г), вычисляем их числовые значения.
3. Сопоставляем полученные числа с отрезками, предложенными в правом столбце, находим пары «буква–число» для ответа.

Решение:

Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.

Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.

Число Б. Оно равно: 1,8³=5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.

Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.

Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.

---

Вариант 17МБ13

[su_note note_color=»#defae6″]

Число m равно √0,15.

Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.

[/su_note]

Алгоритм выполнения

1. Преобразуем число m так, чтобы вынести значение из-под корня.
2. Подставляем последовательно полученную величину для m в каждое из выражений в левом столбце. Получаемые результаты соотносим с подходящим отрезком из правого.

Решение:

Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь корень. Делая подобное приближение – всего на 0,01 – мы не выходим за пределы приемлемой абсолютной погрешности. Поэтому имеем право принять, что √0,15≈√0,16=0,4.

Находим значения выражений А–Г и определяем их соответствия отрезкам:

А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.

Б. 0,4²=0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.

В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.

Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.

Вариант семнадцатого задания 2019 года (10)

[su_note note_color=»#defae6″]

На координатной прямой отмечено число m и точки А, В, С и D.

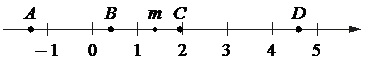
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

[/su_note]

Алгоритм выполнения

1. Определяем приблизительное значение для m.
2. Вычисляем значения выражений 1–4, находим соответствие между полученными результатами и точками А–D на координатной прямой.

Решение:

Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.

Определяем соответствие чисел и точек на прямой:

1. 6–1,4=4,6. Это значение отображено точкой D. Ответ: D–1.
2. 1,4²=1,96. Такое число отображается в точке С. Ответ: С–2.
3. 1,4–1=0,4. Это число соответствует точке В. Ответ: В–3.
4. Здесь можно не вычислять результат, поскольку имеет место единственное отрицательное число, а на прямой обозначена единственная точка слева от 0 – т.А. Ответ: А–4.