Задание №2 ЕГЭ по математике базового уровня

---

Операции со степенями

---

[su_box title=»Описание задания» style=»soft» box_color=»#c1e8cc» title_color=»#0c0a0a»]

Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.

Тематика заданий: операции со степенями

Бал: 1 из 20

Сложность задания: ♦◊◊

Примерное время выполнения: 3 мин.

[/su_box]

Теория к заданию №2

Правила обращения со степенями можно представить следующим образом:

Кроме этого, следует напомнить об операциях с дробями:

Теперь можно перейти к разбору типовых вариантов! 🙂

---

Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня

---

Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.

---

Вариант 2МБ1

Алгоритм выполнения:

1. Представить число с отрицательным показателем в виде правильной дроби.
2. Выполнить первое умножение.
3. Представить степени чисел в виде простых чисел, заменив степени их умножением.
4. Выполнить умножение.
5. Выполнить сложение.

Решение:

Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.

То есть: 10^-1 = 1/10¹ = 1/10

Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.

9 · 1/10 = (9 · 1)/10 = 9/10

Первая степень числа всегда есть само число.

10¹ = 10

Вторая степень числа – это число умноженное само на себя.

10² = 10 · 10 = 100

Вычислим значение выражения, учитывая, что

получим:

Ответ: 560,9

---

Вариант 2МБ2

Алгоритм выполнения:

1. Представить первую степень числа в виде целого числа.
2. Представить отрицательные степени чисел в виде правильных дробей.
3. Выполнить умножение целых чисел.
4. Выполнить умножение целых чисел на правильные дроби.
5. Выполнить сложение.

Решение:

Первая степень числа всегда есть само число. (10¹ = 10)

Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.

То есть:

10^-1 = 1/10¹ = 1/10

10^-2 = 1/10² = 1/(10 · 10) = 1/100

Выполним умножение целых чисел.

3 · 10¹ = 3 · 10 = 30

Выполним умножение целых чисел на правильные дроби.

4 · 10^-2 = 4 · 1/100 = (4 ·1)/100 = 4/100

2 · 10^-1 = 2 · 1/10 = (2 · 1)/10 = 2/10

Вычислим значение выражения, учитывая, что

получим:

Ответ: 30,24

---

Вариант 2МБ3

Алгоритм выполнения:

1. Представить степени чисел в виде умножения и вычислить значение степеней чисел.
2. Выполнить умножение.
3. Выполнить сложение.

Решение:

Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.

2⁴ = 2 · 2 · 2 · 2 = 16

2³ = 2 · 2 · 2 = 8

Выполним умножение:

4 · 2⁴ = 4 · 16 = 64

3 · 2³ = 3 · 8 = 24

Вычислим значение выражения:

Ответ: 88

---

Вариант 2МБ4

Алгоритм выполнения:

1. Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
2. Вынести общий множитель за скобку.
3. Выполнить действие в скобках.
4. Представить степень числа в виде умножения и вычислить значение степени числа.
5. Выполнить умножение.

Решение:

Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.

4⁴ = 4 · 4³

Вынесем общий множитель за скобку

3 · 4³ + 2 · 4⁴ = 4³ · (3 + 2 · 4)

Выполним действие в скобках.

(3 + 2 · 4) = (3 + 8) = 11

Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.

4³ = 4 · 4 · 4 = 64

Вычислим значение выражения, учитывая, что

 

получим:

Ответ: 704

---

Вариант 2МБ5

Алгоритм выполнения:

1. Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
2. Вынести общий множитель за скобку.
3. Выполнить действие в скобках.
4. Представить степень числа в виде умножения и вычислить значение степени числа.
5. Выполнить умножение.

Решение:

Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.

5³ = 5 · 5²

Вынесем общий множитель за скобку

2 · 5³ + 3 · 5² = 5² · (2 · 5 + 3)

Выполним действие в скобках.

(2 · 5 + 3) = (10 + 3) = 13

Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.

5² = 5 · 5 = 25

Вычислим значение выражения, учитывая, что

  , а 

получим:

Выполняем умножение в столбик, имеем:

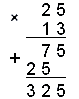
Ответ: 325

---

Вариант 2МБ6

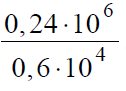
Решение:

В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:

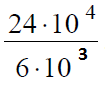
После этого можно выполнить деление 24 на 6, в результате получим 4.

Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:

4 • 10 = 40

Ответ: 40

---

Вариант 2МБ6

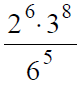
Решение:

В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:

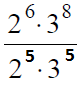
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.

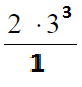
Теперь возводим 3 в куб и умножаем на 2, получая 54.

Ответ: 54

---

Вариант 2МБ6

Алгоритм выполнения

1. Применяем к числителю св-во степеней (а^х)^у=а^ху. Получаем 3^–6.
2. Применяем к дроби св-во степеней a^x/a^y=a^x–y.
3. Возводим 3 в полученную степень.

Решение:

(3^–3)² /3^–8 = 3^–6 /3^–8= 3^{–6–(–8))} = 3^–6+8 = 3² = 9

Ответ: 9

---

Вариант 2МБ7

Алгоритм выполнения

1. Используем для степени в числителе (14⁹) св-во (аb)^х=a^x·b^x. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
2. Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
3. Применяем к дробям св-во степеней a^x/a^y=a^x–y.
4. Находим полученное произведение.

Решение:

14⁹ / 2⁷·7⁸  = (2·7)⁹ / 2⁷·7⁸ = 2⁹·7⁹ / 2⁷ 7⁸ = 2^9–7·7^9–8 = 2²·7¹ = 4·7 = 28

Ответ: 28

---

Вариант 2МБ8

Алгоритм выполнения

1. Выносим за скобки общий множитель 5²=25.
2. Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
3. Выполняем в скобках сложение 10 и 3. Получаем 13.
4. Выполняем умножение общего множителя 25 и 13.

Решение:

2·5³+3·5² = 5²·(2·5+3) = 25·(10+3) = 25·13 = 325

Ответ: 325

---

Вариант 2МБ9

Алгоритм выполнения

1. Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
2. Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
3. Выполняем действия умножения.
4. Получаем разность двух чисел. Находим ее.

Решение:

6·(–1)²+4·(–1)⁵ = 6·1+4·(–1) = 6+(–4) = 6–4 = 2

Ответ: 2

---

Вариант 2МБ10

Алгоритм выполнения

1. Преобразуем множители 10³ и 10² в целые числа.
2. Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
3. Находим результирующую сумму.

Решение:

9,4·10³+2,2·10² = 9,4·1000+2,2·100 = 9400+220 = 9620

Ответ: 9620

---

Вариант 2МБ11

Алгоритм выполнения

1. Преобразуем 10² в целое число и выполняем умножение в числителе путем переноса деся.запятой.
2. Преобразуем 10^–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
3. Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
4. Находим результат путем деления числителя дроби на ее знаменатель.

Решение:

1,6·10² / 4·10^–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 =  16000 / 4 = 4000

Ответ: 40000

---

Вариант 2МБ12

Алгоритм выполнения

1. Применяем к дроби св-ва степеней a^x·a^y=a^x+y и a^x/a^y=a^x–y.
2. Возводим 3 в полученную степень.

Решение:

3^–10·3⁵ / 3^–7 = 3^–10+5  /3^–7 = 3^–5 / 3^–7 = 3^{–5–(–7))} = 3^–5+7 = 3² = 9

Ответ: 9

---

Вариант 2МБ13

Алгоритм выполнения

1. Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (а^х)^у=а^ху, получаем 8¹².
2. Применяем к дроби св-во степеней a^x/a^y=a^x–y.

Решение:

8¹³ /64⁶ =8¹³ / (8²)⁶ =8¹³ /8¹² = 8^13–12 = 8¹ = 8

Ответ: 8

---

Вариант 2МБ14

Алгоритм выполнения

1. Преобразуем степени в числителе дроби и в делителе (число 9²) так, чтобы получились степени с основанием 3.
2. Используем св-во степеней (а^х)^у=а^ху для преобразованных степеней.
3. Используем св-во степеней a^x/a^y=a^x–y.
4. Возводим 3 в полученную степень.

Решение:

27⁴ /3⁶ : 9² =(3³)⁴ / 3⁶ : (32)2 = 3¹²/36 : 3⁴ = 3^12–6–4 = 3² = 9

Ответ: 9

---

Вариант 2МБ15

Алгоритм выполнения

1. Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
2. Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
3. Умножаем 10 на 4.

Решение:

(0,1)²·10³·2² = 0,01·1000·4 = 10·4 = 40

Ответ: 40