Задание №3 ОГЭ по физике

Энергия, импульс и законы их сохранения. Работа. Мощность.

Для решения задания № 3 требуется знание физ. величин и формул, связанных с понятием механической энергии и импульса. Это и собственно понятия энергии и импульса, и законы сохранения для этих величин, а также понятия механической работы и мощности, которые нередко вычисляются именно с их использованием. Полезные сведения, необходимые для решения, приведены в разделе теории.

Теория к заданию №3 ОГЭ по физике

Импульс

Под импульсом в физике понимают количество движения, т.е. импульс представляет собой величину, являющуюся мерой механического движения. Различают импульс тела и импульс силы.

Обозначается величина лат. буквой р. Количественно импульс тела определяется как произведение массы тела на его скорость, т.е.  . Импульс силы определяется как  . Обе величины – векторы. Связь между ними существует самая прямая, а именно: импульс силы равен изменению импульса тела (  ).

Устанавливается эта связь на основании 2-го з-на Ньютона:

  .

Единицей измерения импульса тела и силы является соответственно:  и  .

Закон сохранения импульса

Геометрическая сумма импульсов замкнутой системы тел является неизменной при любых их взаимодействиях и при любом их движении. При этом система тел называется замкнутой, если имеет место только их взаимодействие между собой и исключено их взаимодействие с другими телами (или системами тел).

Уравнение закона:

 ,

где m1 и m2 – массы тел, v1 и v2 – скорости тел до взаимодействия v1’ и v2’ – скорости тел после взаимодействия.

Реактивное движение

Реактивное движение представляет собой интересный случай практической демонстрации з-на сохранения импульса. Заключается оно в том, что от физ.тела отделяется какая-то его часть и начинает двигаться с собственной скоростью. При этом за счет отброса части своей массы это тело приобретает ускорение, направленное в сторону, противоположную направлению, в котором эта часть массы отошла.

С точки зрения з-на сохранения импульса реактивное движение объясняется довольно просто. Если начальный импульс равен нулю (а это так, поскольку пока часть не отделилась, никаких взаимных движений не происходит), то это означает нач.нулевую скорость тела при наличии его массы. Когда масса тела меняется, то компенсироваться это должно за счет соответствующего повышения скорости, потому что необходимо, чтобы импульс системы «оставшаяся + отделившаяся часть тела» по-прежнему остался равным нулю.

Энергия

В механике различают 2 вида энергии – кинетическую и потенциальную. Кинетическая, по сути, характеризует тело в движении, потенциальная – в покое.

Количественно кинетическая энергия определяется по формуле:

 ,

где m – масса тела, v – его скорость.

Потенциальную энергию вычисляют так:

 ,

где m – масса тела, g – ускорение свободного падения, h – высота, на которую тело поднято относительно принятого нулевого уровня в гравитационном поле.

Таким образом, потенциальная энергия – это энергия физ.тела, поднятого над землей.

Закон сохранения энергии

Механическая (полная) энергия имеет свойство сохраняться в замкнутых системах тел. Закон сохранения при этом имеет такую формулировку: полная энергия замкнутой с-мы тел, которые взаимодействуют силами упругости или тяготения, остается постоянной вне зависимости от движений тел в этой системе. В рамках взаимодействия тел один вид энергии может переходить в другой.

В общем виде з-н сохранения выражается уравнением:

 ,

где  и  – соответственно кинетич. и потенц.энергии системы в некий определенный момент времени, а  и  – в другой момент времени.

Используя формулы для вычисления энергий, з-н сохранения энергии можно записать так:  .

Механическая работа

Механическая работа – одна из энергетических параметров движения. Иначе эту величину называют работой силы. Работа является количественной мерой воздействия на тело силы или комплекса сил.

Работа является скалярной (не векторной) величиной. Определяется она по формуле:

 ,

где F – сила, совершающая работу, s – перемещение тела под воздействием силы, α – угол между  и  .

Ед.изм.работы – джоуль (Дж).

Мощность

Мощность – физ.величина, характеризующая быстроту выполнения производимой телом работы. Формула для вычисления мощности, следующая из ее определения, такова:

 ,

где А – выполненная работа, t – время, за которое она выполнена.

Ед.изм.мощности – ватт (Вт).

Из формулы для вычисления мощности следует еще одна – альтернативная – единица измерения работы: [Вт·с]. Этой единицей обычно пользуются, когда необходимо выразить крупные величины работы. Так, общее распространение получили кратная этой единице величина киловатт-час (кВт·ч), используемая при подсчете потребленной электроэнергии.

Разбор типовых вариантов заданий №3 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

Какое(-ие) из утверждений верно(-ы)?

Сила всемирного тяготения между Землёй и Луной

А. зависит от масс Земли и Луны.

Б. является причиной вращения Луны вокруг Земли.

  1. только А
  2. только Б
  3. ни А, ни Б
  4. ни А, и Б

[/su_note]

Алгоритм решения:
  1. Анализируем 1-е утверждение (А). Для этого используем уравнение закона всемирного тяготения. Определяем его истинность.
  2. Анализируем 2-е утверждение (Б). Определяем его истинность.
  3. Выбираем правильный вариант ответа.
  4. Записываем ответ.
Решение:
  1. Согласно закону всемирного тяготения 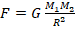 , где М1 и М2 – массы соответственно Земли и Луны. Поскольку массы входят в формулу, то это значит, что зависимость силы от их величин существует. Причем т.к. М1 и М2 находятся в числителе формулы, то зависимость является прямой пропорциональной. Вывод: утверждение А истинно.
  2. Очевидно, что вращение одного тела вокруг другого подразумевает наличие неких сил их взаимодействия. В случае взаимодействия двух планет это гравитационная сила, причем она является единственной. Применив 2-й з-н Ньютона, получаем, что эта сила F равна: 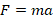 . Направлена она вдоль оси, соединяющие центры планет, т.е. к центру Земли. Следовательно, в данном случае  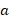– центростремительное ускорение, и движение Луны является равномерным движением по окружности, т.е. имеет место вращение вокруг Земли. Делаем вывод: утверждение Б верно.
  3. Таким образом, оба утверждения верны и правильный ответ – под номером 4.

Ответ: 4

Первый вариант (Камзеева, № 4)

[su_note note_color=»#defae6″]

Проекция скорости тела массой 2 кг, движущегося вдоль оси Ох, изменяется по закону:

 (единицы всех величин даны в системе СИ).

Определите модуль изменения импульса тела через 2 с от начала движения.

  1. 28 кг·м/с
  2. 14 кг·м/с
  3. 8 кг·м/с
  4. 4 кг·м/с

[/su_note]

Алгоритм решения:
  1. Определяем величину импульса в начальный момент времени (при t=0).
  2. Вычисляем импульс для t=2с.
  3. Находим изменение импульса.
  4. Записываем правильный вариант ответа.
Решение:
  1. В момент начала движения 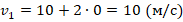 . Отсюда:  .
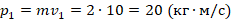  2. Через 2с после начала движения 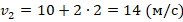 . Получаем:  .
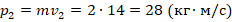  3. Тогда изменении импульса: 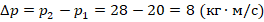  . Соответственно, правильный ответ – под номером 3.

Ответ: 3

Второй вариант (Камзеева, № 6)

[su_note note_color=»#defae6″]

Мяч бросают вертикально вверх с поверхности Земли. Сопротивлением воздуха можно пренебречь. При увеличении массы бросаемого мяча в 3 раза высота подъема мяча

  1. не изменится
  2. увеличится в √3 раза
  3. увеличится в 3 раза
  4. увеличится в 9 раз.

[/su_note]

Алгоритм решения:
  1. Определяем зависимость высоты подъема от массы мяча.
  2. Определяем формулу для вычисления подъема. Находим вариант правильного ответа.
  3. Записываем ответ.
Решение:
  1. При условии, что сопротивлением воздуха можно пренебречь, на мяч, подброшенный вверх, действует единственная сила – сила тяжести. Ее величина одинакова на любой высоте. Следовательно, высота подъема от массы не зависит.
  2. Высота подъема с поверхности Земли для тела, движущегося под действием только силы тяжести, должна быть вычислена на основании уравнения ОЗМ: 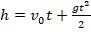 . Из него следует, что высота подъема зависит только от нач.скорости v0. Поскольку в условии об изменении нач.скорости не сказано, то можем утверждать, что она не изменилась. А это означает, что высота подъема тоже не изменилась. Таким образом, правильный вариант ответа – под номером 1.

Ответ: 1

Третий вариант (Камзеева, № 8)

[su_note note_color=»#defae6″]

Мяч массой 0,1 кг подбросили вертикально вверх. В результате мяч поднялся на высоту 4 м, а затем упал обратно на землю. Чему равна работа силы тяжести на всем пути мяча?

  1. 0 Дж
  2. 4 Дж
  3. –0,4 Дж
  4. –4 Дж

[/su_note]

Алгоритм решения:
  1. Записываем формулы для вычисления работы и для силы тяжести. Выводим из них уравнение для расчета работы.
  2. Вычисляем работу при подъеме мяча вверх.
  3. Вычисляем работу при последующем падении мяча на землю. Находим суммарную работу.
  4. Записываем ответ.
Решение:
  1. Работа вычисляется по формуле: 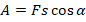 , где s – высота подъема мяча. Сила тяжести:  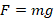 . Отсюда получим:  .
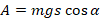  2. Когда мяч летит вверх, вектор его перемещения направлен вертикально вверх. Вектор ускорения своб.падения всегда направлен вертикально вниз. Следовательно, угол между этими векторами α составляет 1800. Т.к. 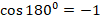 , то  .
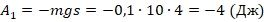  3. Когда мяч летит вниз, вектор его перемещения направлен вертикально вниз и, соответственно, совпадает с вектором ускорения своб.падения. Это значит, что 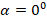 и 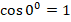 . Тогда  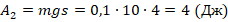. Суммарная работа:  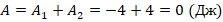. Правильный ответ – под номером 1.

Ответ: 1

Текст: Базанов Даниил, 6.3k 👀