Задание №4 ЕГЭ по математике базового уровня

Преобразование выражений

[su_box title=»Описание задания» style=»soft» box_color=»#c1e8cc» title_color=»#0c0a0a»]

В задании №4 ЕГЭ по математике базового уровня нам необходимо продемонстрировать умения работы с выражениями. В данных задачах необходимо выразить из заданного выражения нужную переменную и вычислить её, подставив значения.

Тематика заданий: преобразования выражений

Бал: 1 из 20

Сложность задания: ♦◊◊

Примерное время выполнения: 3 мин.

[/su_box]

Разбор типовых вариантов заданий №4 ЕГЭ по математике базового уровня

Вариант 4МБ1

[su_note note_color=»#defae6″]

Найдите v0 из равенства v = v0 + at, если v = 20, t = 2, a = 7.

[/su_note]

Алгоритм выполнения:
  1. Подставить данные значения в выражение.
  2. Решить уравнение относительно неизвестной.
Решение:

Подставим все значения в данное выражение, получим:

20 = v0 + 7 · 2

Преобразуем:

20 = v0 + 14.

Найдем неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

v0 = 20 – 14

v0 = 6

Ответ: v0 = 6

Вариант 4МБ2

[su_note note_color=»#defae6″]

Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле  image001 . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.

[/su_note]

Алгоритм выполнения:
  1. Подставить все значения в данную формулу.
  2. Произвести вычисления.
Решение:

По условию задания дана высота h=0,9 м и ускорение свободного падения g=9,8 м/с2. Подставим эти значения в формулу вычисления скорости v, получим:

image002

Делаем умножение 1,8 на 9,8, имеем:

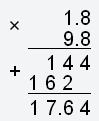
image003

Примечание: При умножении в столбик десятичных дробей запятая записывается строго под запятой. В полученном результате справа отсчитывают столько знаков, сколько поле запятой в ОБЕИХ дробях ВМЕСТЕ.

и извлекаем из числа 17,64 квадратный корень:

image004  м/с.

Ответ: 4,2 м/с.

Вариант 4МБ3

[su_note note_color=»#defae6″]

Энергия заряженного конденсатора W (в Дж) вычисляется по формуле  image001 , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью  image002  Ф, если заряд на его обкладке равен 0,019 Кл.

[/su_note]

Алгоритм выполнения задания:
  1. Подставить все известные значения в данную формулу.
  2. Провести вычисления.
Решение:

Подставим в формулу энергии конденсатора значения q=0,019 Кл и C =  image002  Ф, получим:

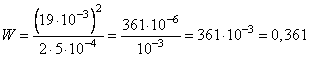
image003

Пояснения:

Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (19 · 10-3)2 = 192 · 10-3·2.

Чтобы найти вторую степень числа нужно умножить число само на себя.

192 = 19 · 19 = 361

Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.

361 · 10-3 = 361/1000 = 0,361

Ответ: 0,361.

Вариант 4МБ4

[su_note note_color=»#defae6″]

Энергия заряженного конденсатора W (в Дж) вычисляется по формуле  image001 , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью  image002  Ф, если заряд на его обкладке равен 0,07 Кл.

[/su_note]

Алгоритм выполнения:
  1. Подставить все известные значения в данную формулу.
  2. Провести вычисления.
Решение:

Подставим в формулу энергии конденсатора значения q=0,07 Кл и C =  image002  Ф, получим:

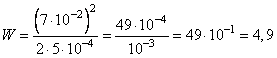image003 .

Пояснения:

Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (7 · 10-2)2 = 72 · 10-2·2.

Чтобы найти вторую степень числа нужно умножить число само на себя.

72 = 7 · 7 = 49

Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.

49 · 10-1 = 49/10 = 4,9

Ответ: 4,9.

Вариант 4МБ5 (демо)

[su_note note_color=»#defae6″]

Найдите m из равенства F = ma, если F = 84 и a = 12.

[/su_note]

Алгоритм выполнения:
  1. Подставить данные значения в выражение.
  2. Решить уравнение относительно неизвестной.
Решение:

Подставим все значения в данное выражение, получим:

84 = m ·12

2. Найдем неизвестный множитель. Чтобы найти неизвестный множитель нужно разделить произведение на известный множитель.

m = 84 : 12

m = 7

Ответ: 7 кг.

Вариант 4МБ6 (ЕГЭ 2017)

[su_note note_color=»#defae6″]

Найдите m из равенства F = ma , если F = 84 и a =12.

[/su_note]

В начале выразим из формулы m, так как это множитель, то он равен произведению, деленному на второй множитель.

m=F/a

Теперь можем подставить числа из условия:

m=84/12=7

Ответ: 7

Вариант 4МБ7

[su_note note_color=»#defae6″]

Найдите v0 из равенства v = v0 + at , если v = 20 , t = 2 и a = 7 .

[/su_note]

Аналогично выразим v0, перенеся at в левую часть:

v — at = v0

Подставим значения:

20 — 7 • 2 = 6 = v0

Ответ: 6

Вариант 4МБ8

[su_note note_color=»#defae6″]

Найдите S из равенства S = v0t + at2/2 , если v0 = 6 , t = 2 , a = −2.

[/su_note]

В данном случае нам необходимо просто подставить числа и выполнить вычисления:

S = 6 • 2 + (-2) • 22/2 = 12 -4 = 8

Ответ: 8

Вариант 4МБ9

[su_note note_color=»#defae6″]

Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула , где tC – температура в градусах по шкале Цельсия, tF – температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует 95 градусов по шкале Фаренгейта?

[/su_note]

Алгоритм выполнения
  1. Подставляем данное в условии для tF значение, равное 95, в формулу для tC.
  2. Выполняем числовые расчеты в формуле в такой последовательности: 1) вычитание в скобках; 2) внесение в числитель дроби 5/9 полученной в скобках разности; 3) сокращение 63 в числителе и 9 в знаменателе на 9; 4) нахождение конечного результата.
Решение:

Вычисляем вычитание в скобках:

95-32=63

Далее умножаем на 5/9, замечаем, что 63 делится на 9 — это 7, что и умножаем на 5, получаем 35!

Ответ: 35

Вариант 4МБ10

[su_note note_color=»#defae6″]

Кинетическая энергия (в джоулях) вычисляется по формуле , где m – масса тела (в килограммах), а v – его скорость (в м/с). Пользуясь этой формулой, найдите E (в джоулях), если v=4 м/с и m=10 кг.

[/su_note]

Алгоритм выполнения
  1. Подставляем числовые данные из условия в формулу для Е.
  2. Производим вычисления. Сначала возводим v в квадрат (получаем 16). Затем сокращаем 16 в числителе и 2 в знаменателе на 2. Далее выполняем умножение.

Решение:

Возводим 4 в квадрат — это 16, умножаем на 10 — 160 и делим на 2 — 80 — вот и ответ!

Ответ:80

Вариант 4МБ11

[su_note note_color=»#defae6″]

Ускорение тела (в м/с2) при равномерном движении по окружности можно вычислить по формуле , где ω – угловая скорость вращения (в с–1), а R – радиус окружности (в метрах). Пользуясь этой формулой, найдите а (в м/с2), если R=4 м и ω=7 с–1.

[/su_note]

Алгоритм выполнения
  1. Подставляем в формулу числовые значения для R и ω.
  2. Делаем вычисления в полученном числовом выражении: 1) возводим в квадрат 7; 2) выполняем умножение.
Решение:

Если R=4 и ω=7, то а = 72 · 4 = 49 · 4 = 196 (м/с2)

Ответ:196

Вариант 4МБ12

[su_note note_color=»#defae6″]

Мощность постоянного тока (в ваттах) вычисляется по формуле , где U – напряжение (в вольтах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R= 6 Ом и U=12 В.

[/su_note]

Алгоритм выполнения
  1. Поскольку все числовые данные приведены в условии в соответствии с СИ, то просто подставляем эти числа в формулу для мощности.
  2. Вычисляем значение для Р: 1) в числителе 122 представляем как 12·12; 2) выполняем сокращение на 6; 3) находим произведение.
Решение:

Возводим 12 в квадрат — это 144, затем делим на 6 — это 24. Либо замечаем, что 12 можно сократить на 6 — это 2, тогда умножаем оставшуюся от квадрата 12 на 2 — снова получаем 24.

Ответ:24

Вариант 4МБ13

[su_note note_color=»#defae6″]

Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s=nl, где n – число шагов, l – длина шага. Какое расстояние прошел человек, если l=50 см, n=1600? Ответ дайте в метрах.

[/su_note]

Алгоритм выполнения
  1. Т.к. ответ требуется дать в метрах, то l тоже необходимо перевести в метры.
  2. Числовые данные подставляем в формулу для s.
  3. Производим умножение.

Решение:

l=50 см=0,5 м

Если l=0,5 n=1600, то s=0,5·1600=800 (м)

Ответ:800

Вариант 4МБ14

[su_note note_color=»#defae6″]

Закон Гука можно записать в виде F=kx, где F – сила (в ньютонах), с которой растягивают пружину, х – абсолютное удлинение пружины (в метрах), а k – коэффициент упругости. Пользуясь этой формулой, найдите х (в метрах), если F=51 Н и k=3 Н/м.

[/su_note]

Алгоритм выполнения
  1. Из приведенной в условии формулы выражаем искомое удлинение х.
  2. В полученную формулу подставляем данные в условии числовые величины.
  3. Делаем вычисление.

Решение:

Искомое удлинение x находим как частное — F/k, так как x множитель.

Подставляя значения, получаем:

51/3=17

Ответ:17

Вариант 4МБ15

[su_note note_color=»#defae6″]

Работа постоянного тока (в джоулях) вычисляется по формуле, где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t=5 с, I=2 А и R=13 Ом.

[/su_note]

Алгоритм выполнения
  1. Подставляем в формулу приведенные в условии соответствующие числовые данные.
  2. Производим вычисления. Делаем это оптимальным способом: сначала находим I2, потом умножаем полученное число на значение для t, и уже затем множим это произведение на значение для R.

Решение:

Если I=2 А, R=13 Ом, t=5 с, то А=22·13·5=4·13·5=(4·5)·13=20·13=260 (Дж)

Ответ:260

Вариант 4МБ16

[su_note note_color=»#defae6″]

Сумма углов выпуклого многоугольника вычисляется по формуле , где n – количество его углов. Пользуясь этой формулой, найдите n, если ∑=15π.

C:UsersКсеньяDesktopматме8.jpg

[/su_note]

Алгоритм выполнения
  1. Преобразовываем формулу и выражаем из нее искомое n.
  2. Подставляем в полученное уравнение формулу ∑=15π.
  3. Выполняем сокращение на π. Находим конечный результат.

Решение:

Из ∑=(n–2)π имеем: n–2=∑/π → n=∑/π+2.

Если ∑=15π, то получаем:

15π/π +2 = 17

Ответ:17

Вариант 4МБ17

C:UsersКсеньяDesktopматме9.jpg

[su_note note_color=»#defae6″]

Среднее геометрическое трех чисел a, b и c вычисляется по формуле . Вычислите среднее геометрическое чисел 2, 4, 27.

[/su_note]

Алгоритм выполнения
  1. Подставляем в формулу числовые данные из условия.
  2. В подкоренном выражении представляем 4 как 22, а 27 как 33.
  3. Произведение 2·22 представляем как 23. Получаем две степени с показателем 3.
  4. Выносим степени из-под куб.корня. Получаем произведение оснований этих степеней. Вычисляем произведение.
Решение:

2 при умножении на 4 дает 2 в кубе, а 27 — это три в кубе. По свойству корней избавляемся от кубического корня и степеней для 2 и 3 поочередно (просто сокращая корень на степень), а затем выполняем умножение 2 на 3 — получаем 6.

Ответ:6

Вариант 4МБ18

C:UsersКсеньяDesktopматме10.jpg

[su_note note_color=»#defae6″]

Площадь треугольника вычисляется по формуле , где b и c – две стороны треугольника, а α – угол между ними. Пользуясь этой формулой, найдите площадь S, если b=18, c=16 и sinα=1/3.

[/su_note]

Алгоритм выполнения
  1. Подставляем в формулу приведенные в условии числовые данные.
  2. Заводим 18 и 16 в числитель, получаем дробь с числителем и знаменателем в виде произведений, соответственно, чисел 18, 16 и 2,3.
  3. Сокращаем 18 и 3 на 3, а 16 и 2 на 2. Получаем в знаменателе 1, а в числителе произведение 6 и 8. Находим это произведение.

Ответ:48

Текст: Базанов Даниил, 10.5k 👀