Начала теории вероятностей
В задании №4 профильного уровня ЕГЭ по математике необходимо решить простую задачу по теории вероятностей. Задача совсем простая, достаточно поделить одно число на другое, ну или перед этим вычесть из одного числа другое. Задание интуитивно понятно, и решить его можно даже не зная основных формул комбинаторики. Разберем несколько примеров.
Разбор типовых вариантов заданий №4 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=»#defae6″]
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
[/su_note]
Алгоритм решения:
- Обозначаем событие А.
- Определяем число всех событий.
- Находим число благоприятствующих исходов.
- Подсчитываем вероятность.
- Записываем ответ.
Решение:
1. Пусть А –событие, при котором ученику попадает билет с вопросом о грибах.
2. Всего билетов 25, значит всех событий n=25.
3. Благоприятствующих исходов m=2, т.к. только 2 билета содержат вопрос о грибах.
4. Вероятность события А равна Р(А) = m/n=2/25 = 0,08.
Ответ: 0,08.
Второй вариант задания (из Ященко, №1)
[su_note note_color=»#defae6″]
В среднем из 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
[/su_note]
Алгоритм решения:
- Обозначим событие «купленный контрольный насос не подтекает» буквой А.
- Найдем число всех событий.
- Найдем число благоприятствующих событий.
- Определим вероятность события А.
- Запишем ответ.
Решение:
1. Пусть событие А: выбранный случайным образом насос не протекает.
2. Число всех событий n=600.
3. Число благоприятствующих исходов равно m=600-3=597. Тогда вероятность того, что выбранный насос не подтекает, определяется так:
m/n = 597/600 = 0,995
Ответ: 0,995
Третий вариант задания (из Ященко, №7)
[su_note note_color=»#defae6″]
В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
[/su_note]
Алгоритм решения:
- Обозначим событие «на вызов придет желтая машина» буквой А.
- Найдем число всех возможных событий.
- Найдем число благоприятствующих событий.
- Вычислим вероятность события А.
- Запишем ответ.
Решение:
1. Пусть событие А: на вызов придет желтое такси.
2. Число всех событий n=60.
3. Число благоприятствующих исходов равно m=60-27= 33. Тогда вероятность того, что выбранное для поездки будет желтым, определяется так:
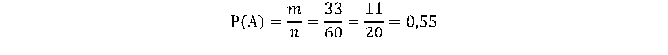
Ответ: 0,55.
Четвертый вариант задания (из Ященко, №21)
[su_note note_color=»#defae6″]
На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
[/su_note]
Алгоритм решения:
- Обозначим х число всех тарелок, произведенных на фабрике.
- Найдем число дефектных тарелок.
- Найдем число всех изымаемых при проверке тарелок.
- Определим вероятность события А: куплена качественная тарелка.
- Запишем ответ.
Решение:
1. Пусть на фабрике изготовлено х тарелок.
2. Бракованных тарелок на фабрике изготовлено 20%. Это всего 0,2x штук. Тогда в торговую сеть поступает 0,8х качественных тарелок.
3. При проверке качества изымается 70% бракованных тарелок, значит, из них 30% поступает в продажу. Получается, на прилавок идет 0,2x · 0,3 = 0,06x бракованных.
Всего в торговую сеть поступает 0,8x + 0,06x = 0,86x тарелок.
4. Пусть событие А: купленная тарелка качественная. Тогда число благоприятствующих событий m=N(A) = 0,8x. Всего число исходов n = 0,86x.
5. Вероятность события А определяем формулой вероятности: P(A) = m/n = 0,8x/0,86x = 0,9302325… ≈ 0,93
Ответ: 0,93.