Задание №5 ЕГЭ по математике базового уровня

---

Значение выражений

---

[su_box title=»Описание задания» style=»soft» box_color=»#c1e8cc» title_color=»#0c0a0a»]

В задании №5 ЕГЭ по математике базового уровня нам необходимо вычислить значение выражения, пользуясь различными правилами: формулами сокращенного умножения, знаниями тригонометрии, свойствами логарифмов и другими. Данное задание требует более глубоких знаний и значительно сложнее первого задания, где достаточно было знать элементарные математические операции.

Тематика заданий: значение выражений

Бал: 1 из 20

Сложность задания: ♦♦♦

Примерное время выполнения: 5-7 мин.

[/su_box]

Теория к заданию №5

В данном задании, кроме операций со степенями, о которых мы говорили в прошлых заданиях, необходимо помнить формулы сокращенного умножения:

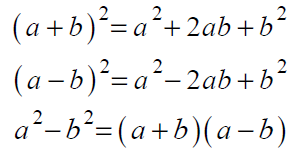
Кроме этого, очень часто встречаются задания на знания свойств логарифма:

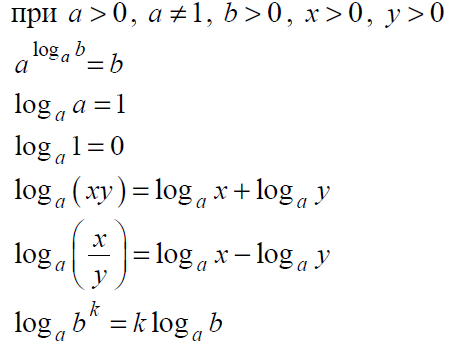
Полезными будут представления о тригонометрической окружности, по которой можно определять знаки тригонометрических функций:

---

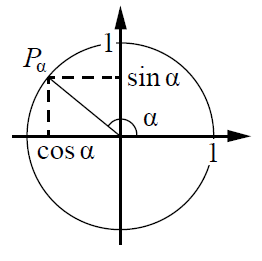
Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

---

Во всех заданиях необходимо найти значение выражения.

---

Вариант 5МБ1

Алгоритм выполнения

1. Представим угол 390° с учетом периодичности функции tg меньшим углом.
2. Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
3. Выполним умножение.

Решение:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть tg α = tg (α + 180°) = tg (α — 180°)

tg 390° = tg (390° — 180°) = tg 210° = tg (210° — 180°) = tg 30°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 30° = √3/3

Подставим найденное значение в данное выражение.

20 · √3 · (√3/3) = (20 · √3 · √3)/3 = (20 · 3)/3 = 20

Решение в общем виде

Вычислим выражение, учитывая, что функция тангенс периодическая с периодом π радиан или 180°. Следовательно, угол 390° эквивалентен углу

и получаем выражение:

 

 

Ответ: 20.

---

Вариант 5МБ2

Алгоритм выполнения

1. Представим угол 420° с учетом периодичности функции tg меньшим углом.
2. Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
3. Выполним умножение.

Решение №1:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть

tg α = tg (α + 180°) = tg (α — 180°)

tg 390° = tg (420° — 180°) = tg 240° tg (240° — 180°) = tg 60°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 60° = √3

Подставим найденное значение в данное выражение.

-50 · √3 · √3 = -50 · 3 = -150

Решение №2:

Заметим, что функция тангенс периодическая с периодом π радиан или 180°. Поэтому, тангенс угла 420° эквивалентен тангенсу угла в

,

получаем:

 

 

Ответ: -150.

---

Вариант 5МБ3

Алгоритм выполнения

1. Объединим подкоренные выражения под один корень.
2. Внесем под корень дробь.
3. Сократим дробь под корнем.
4. Представим произведение под корнем в виде произведения вторых степеней.
5. Вынесем из под корня множители.
6. Выполним умножение.

Решение:

Объединим подкоренные выражения под один корень. Имеем право так сделать использовав, свойство квадратного корня.

5/3 · √27 · √3 = 5/3 · √(27 · 3)

 

 

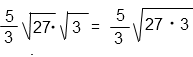
Внесем под корень дробь.

Корень квадратный, следовательно, чтобы внести дробь под знак корня нужно возвести ее в квадрат. То есть умножить сам на себя числитель и знаменатель.

(5/3)² = (5 · 5)/(3 · 3)

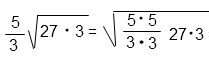
Сократим дробь под корнем на три дважды.

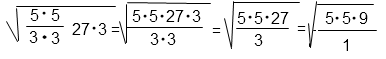
Представим произведение под корнем в виде произведения вторых степеней.

 

 

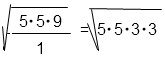
Вынесем из под корня множители и выполним умножение.

 

 

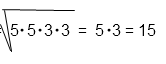
Решение в общем виде:

 

 

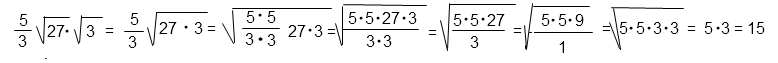
Ответ: 15.

---

Вариант 5МБ4

[su_note note_color=»#defae6″]

Найдите cos α, если sin α = 0,8 и 90° ‹ α ‹ 180°.

[/su_note]

Алгоритм выполнения

1. Запишем основное тригонометрическое тождество.
2. Подставим в основное тригонометрическое тождество все известные данные.
3. Решим полученное уравнение относительно cos α.
4. Выбрать корни, подходящие к условию задания.

Решение:

Запишем основное тригонометрическое тождество.

sin² α + cos² α = 1

Подставим в основное тригонометрическое тождество все известные данные.

0,8² + cos² α = 1

Решим полученное уравнение относительно cos α.

cos² α – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

cos² α = 1 — 0,8²

Чтобы найти вторую степень числа нужно число умножить само на себя.

0,8² = 0,8 · 0,8 = 0,64

cos² α = 1 — 0,8² 1 — 0,64 = 0,36

cos α = √0,36

cos α = 0,6 или -0,6

Условие 90° ‹ α ‹ 180° означает, что -1 ‹ соs α ‹ 0.

Следовательно данному условию удовлетворяет только один корень -0,6.

Ответ: -0,6.

---

Вариант 5МБ5

[su_note note_color=»#defae6″]

(2√13 −1)(2√13 +1).

[/su_note]

Алгоритм выполнения

В данном задании необходимо сразу заметить формулу сокращенного умножения — разность квадратов (последняя формула сокращенного умножения в теории выше).

Решение:

После этого, решение задания сводится к следующему:

(2√13 −1)(2√13 +1) = (2√13)² — 1²  = 4 • 13 — 1 = 51

Ответ: 51.

---

Вариант 5МБ6

[su_note note_color=»#defae6″]

5^log₅6+1 .

[/su_note]

Алгоритм выполнения

Сначала вспомним свойства степеней и разложим выражение следующим образом:

5^log₅6 • 5¹

Затем вспомним определение и свойство логарифма — это вторая строчка из нашей теории:

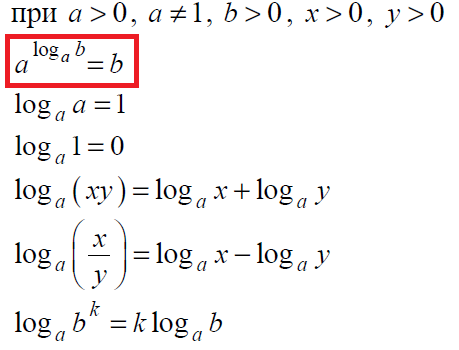
Решение:

 Получим:

6•5 = 30

Ответ: 30

---

Вариант 5МБ7

[su_note note_color=»#defae6″]

(√11-√3)(√11+√3)

[/su_note]

Алгоритм выполнения

1. Применяем формулу сокращенного умножения a²–b²=(a-b)(a+b).
2. Используем определение кв.корня: (√a)²=a.
3. Находим полученную разность целых чисел.

Решение:

Исходя из алгоритма, подставляем а=√11, а b=√3, тогда 11-3=8

Ответ: 8

---

Вариант 5МБ8

Алгоритм выполнения

1. Применяем тождество log_a(xy)=log_ax+log_ay.
2. Преобразовываем множители, стоящие под знаком логарифма, в степени.
3. Используем для выражения под знаком логарифма св-во степеней a^xb^x=(ab)^x.
4. Используем св-во логарифмов xlog_ab=log_ab^x.
5. Применяем тождество log_aa=1,.

Решение:

log₆27 + log₆8 = log₆27·8 = log₆3³·2³ = log₆(3·2)³ = log₆6³ = 3log₆6 = 3

Ответ:3

---

Вариант 5МБ9

Алгоритм выполнения

1. Вносим множитель √6 в скобки.
2. Выполняем умножение √24 и √6. Получим √144. Это число является полным квадратом: (√12)².
3. Перемножаем √6 и √6. Получаем (√6)².
4. Используя определение кв.корня (√а)²=а, находим, что (√12)²=12, а (√6)²=6.
5. Находим разность полученных целых чисел.

Решение:

Ответ: 6

---

Вариант 5МБ10

Найдите sinα, если

Алгоритм выполнения

1. Применим основное тригонометрическое тождество. В тождество подставим данное в условии числовое значение для косинуса.
2. Выполняем преобразование тождества, получаем числовой результат.
3. Определяем знак результата, исходя из величины угла α.

Решение: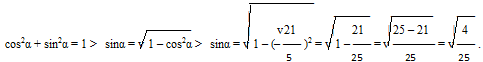

Ответ: 0,4

---

Вариант 5МБ11

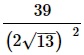
Алгоритм выполнения

1. Выполняем 1-ю по приоритетности операцию – возведение в степень (в знаменателе). Для этого используем св-во степеней (ab)²=a²·b². Далее для множителя (√13)² применяем формулу, определяющую понятие кв.корня: (√а)²=а.
2. Выполняем умножение в знаменателе.
3. Представляем число 39 в числителе как произведение 3·13.
4. Сокращаем дробь на 13.
5. Переводим полученную обыкновенную дробь в десятичную.

Решение: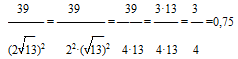

Ответ: 0,75

---

Вариант 5МБ12

Алгоритм выполнения

1. Применяем к показателю степени 2log₃7 св-во логарифмов log_b^ya^x=(x/y)log_ba. Получим log₃7².
2. Применяем св-во логарифмов a^log_a^b=b. В результате знак логарифма исчезает, остается только выражение 7², которое было под знаком логарифма.
3. Возводим 7 в квадрат.

Решение:

2log₃7 log₃7²

3 = 3 = 7² = 49

Ответ:49

---

Вариант 5МБ13

Алгоритм выполнения

1. Используем св-во корней √(a·b)=√a·√b. Таким способом √63 разложим на множители √9 и √7.
2. Сгруппируем одинаковые множители √7. Получим (√7)².
3. Основываясь на определении кв.корня (√а)²=а, представляем √9=(√3)².
4. Возводим полученные числа в квадрат.
5. Находим итоговое произведение.

Решение: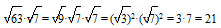

Ответ: 21

---

Вариант 5МБ14

Алгоритм выполнения

1. Используем св-во степеней x^a+b=x^a·x^b. Получим 2 множителя, первый из которых равен 7, а второй представляет собой степень с основанием 7 и показателем, содержащим логарифм.
2. Для второго множителя применим св-во логарифмов a^loga^b=b.
3. Находим результирующее произведение.

Решение:

Ответ: 21

---

Вариант 5МБ15

Алгоритм выполнения

1. Для cos 390⁰ используем ф-лу приведения cos (360⁰+α)=cos α. Получим cos 30⁰=√3/2. Записываем получившееся выражение в виде дроби со знаменателем 2.
2. Вычисляем произведение √3·√3 путем возведения в степень. Для этого используем определение кв.корня: (√а)²=а.
3. Сокращаем 20 в числителе и 2 в знаменателе на 2.
4. Находим конечное произведение.

Решение:

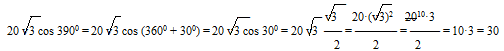
Ответ: 30

---

Вариант 5МБ16

Алгоритм выполнения

1. Преобразовываем часть выражения, взятую в скобки. Для этого представляем 49 как 7². Затем используем св-во логарифмов log_ba^x=xlog_ba, а далее св-во log_aa=1. Получаем 2.
2. Применяем св-во логарифмов log_aa=1.

Решение:

log₂(log₇49) = log₂(log₇7²) = log₂(2log₇7) = log₂2 = 1

Ответ: 1