Задание №5 ОГЭ по физике

Основы гидродинамики

Для успешного решения задания № 5 требуется знание основ гидродинамики. К ним относится понимание процессов, происходящих с жидкостями и телами, контактирующими с жидкостями, сущности физ.величин плотности и давления, а также формул, связывающих их с другими физ.величинами. Необходимая для решения задач такого плана информация имеется в разделе теории.

Теория к заданию №5 ОГЭ по физике

Плотность вещества

Плотностью называют массу вещества, которая приходится на единицу объема. Следовательно, плотностью можно считать удельную массу вещества. Количественно плотность определяют по формуле:

где m – массе вещества, V – его объем.

По этой же формуле вычисляется и средняя плотность. Для расчета при этом берется масса всего вещества и его общий объем.

Давление

Давлением называется: 1) сила, которая воздействует на поверхность твердого тела; 2) степень (сила) упругости жидкости либо газа. По сути, давление – это мера механического напряжения. Эта физ.величина является скалярной.

Давление в физике традиционно обозначается лат.буквой р. Единица измерения давления – паскаль (Па).

Атмосферное давление – это сила воздействия атмосф.столба на все физ.объекты (тела), находящиеся в атмосфере Земли, а также на земную поверхность. Если атмосфера является стационарной и покоящейся, то атмосф.давление на материальный объект соответствует весу столба воздуха над этим объектом, приходящегося на единицу площади. Атмосф.давление измеряется в мм ртутного столба (мм рт.ст.). Нормальным принято давление в 760 мм рт. ст. при t=0ºC. В пересчете на единицы СИ это давление соответствует 101325Па.

Сила Архимеда

На помещенное в жидкость физ.тело воздействует выталкивающая сила, равная по величине силе тяжести, испытываемая этим телом. Причина возникновения архимедовой силы – неодинаковость гидростатического давления в жидкости на различных глубинах. Точка ее приложения называется центром давления, который является центром масс тела (или его части) погруженного в жидкость

Формула для вычисления силы Архимеда:

где ρж – плотность жидкости; V – объем части физ.тела, помещенной в жидкость, или всего тела, если оно погружено в жидкость полностью.

Сообщающиеся сосуды

Сообщающимися считаются сосуды, которые объединены ниже поверхности жидкости в единую систему, причем так, что жидкость может перетекать из одного в другой.

Закон сообщающихся сосудов:

что означает обратную пропорциональную зависимость высоты столбов жидкостей и их плотностей.

Если в сообщающихся сосудах находится жидкость однородная, то высота столбов свободной поверхности жидкости в них совпадает.

Разбор типовых вариантов заданий №5 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

Цилиндр 1 поочередно взвешивают с цилиндром 2 такого же объема, а затем с цилиндром 3, имеющим меньший объем (см. рисунок).

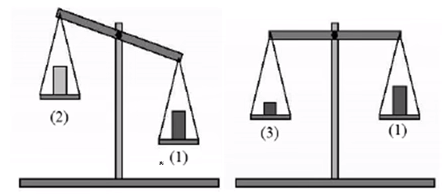
Максимальную среднюю плотность имеет цилиндр

  1. 1
  2. 2
  3. 3
  4. 1 и 3

[/su_note]

Алгоритм решения:
  1. Анализируем условие и рисунок слева (цилиндры 1 и 2). Определяем соотношение плотностей цилиндров.
  2. Анализируем условие и рисунок справа (цилиндры 3 и 1). Делаем вывод относительно соотношения плотностей.
  3. Определяем цилиндр с максимальной плотностью.
Решение:
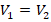
  1. Согласно условию: 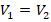. Поскольку на весах слева цилиндр 1 перевешивает 2, то это значит, что 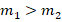. Тогда из уравнения 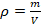следует, что  .
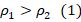  2. По условию 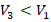 . Поскольку весы справа уравновешены, то это значит, что массы цилиндров равны, и из уравнения для плотности следует:  .
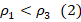  3. Объединив неравенства (1) и (2), получим: 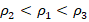. Отсюда: максимальная плотность у 3-го цилиндра.

Ответ: 3

Первый вариант (Камзеева, № 7)

[su_note note_color=»#defae6″]

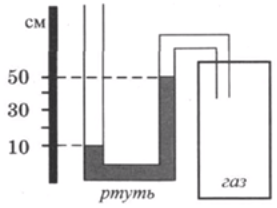
Одно из колен U-образного манометра соединили с сосудом, наполненным газом (см. рис.). Атмосферное давление равно 760 мм рт.ст. Чему равно давление газа в сосуде? В качестве жидкости в манометре используется ртуть.

  1. 1160 мм рт.ст
  2. 500 мм рт.ст.
  3. 360 мм рт.ст.
  4. 100 рт.ст.

[/su_note]

Алгоритм решения:
  1. Анализируем условие и рисунок. Делаем вывод о соотношении атмосф.давления и давления в сообщающихся сосудах.
  2. Определяем искомую величину давления газа.
  3. Фиксируем ответ.
Решение:
  1. На схеме показано, что уровень ртути в 1-м (левом) колене меньше, чем в среднем. Это означает, что атмосф.давление выше давления газа. На шкале на рисунке видно, что разница давлений составляет 40 см. рт. ст., то есть 400 мм. рт. ст.
  2. Имеющаяся разница давлений означает, что давление газа меньше на эту разницу по сравнению с атмосферным давлением, т.е.: p = 760 — 400 = 360 (мм. рт. ст.).

Ответ: 3

Второй вариант (Камзеева, № 10)

[su_note note_color=»#defae6″]

Имеются три сплошных шара одинаковой массы, но изготовленные из разных веществ – из алюминия, стали или свинца. Шары полностью погружают в воду. Выталкивающая сила со стороны воду имеет

  1. наибольшее значение для алюминиевого шара
  2. наибольшее значение для стального шара
  3. наибольшее значение для свинцового шара
  4. одинаковое значение для всех шаров

[/su_note]

Алгоритм решения:
  1. Записываем табличные значения для плотности материалов шаров.
  2. Записываем уравнение з-на Архимеда.
  3. Анализируем уравнение и определяем соотношение для выталкивающей силы для шаров.
  4. Записываем ответ.
Решение:
  1. Плотности материалов шаров: ;   ;   .
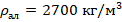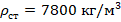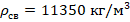  2. Согласно з-ну Архимеда, выталкивающая сила равна: 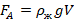. Поскольку по условию шары погружены в жидкость целиком, то V – полный объем шара.
  3. Т.к. во всех 3 случаях жидкость одна и та же (вода), то в уравнении 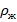 совпадает для всех шаров. Соответственно, максимальная архимедова сила у того из них, который имеет наибольший объем. Объем выразим из формулы для плотности вещества:  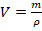. Учитывая оговорку в условии о том, что у шаров одинаковая масса, делаем вывод: чем меньше плотность вещества шара, тем больше выталкивающая сила. Поскольку наименьшую плотность имеет алюминий, то именно на алюминиевый шар действует максимальная выталкивающая сила.

Ответ: 1

Третий вариант (Камзеева, № 12)

[su_note note_color=»#defae6″]

Сосуд частично заполнили водой и уравновесили на рычажных весах (см. рис.).

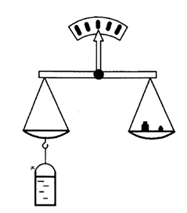
В первом случае в сосуд опустили пробковый шарик, во втором случае – стальной шарик. Нарушится ли равновесие весов?

  1. равновесие нарушится только в первом случае
  2. равновесие нарушится только во втором случае
  3. равновесие нарушится в обоих случаях
  4. в обоих случаях равновесие не нарушится

[/su_note]

Алгоритм решения:
  1. Анализируем 1-й случай. Делаем вывод о положении весов.
  2. Анализируем 2-й случай. Делаем вывод о положении весов.
  3. Находим верный вариант ответа. Записываем его.
Решение:
  1. В 1-м случае – с пробковым шариком – шарик будет плавать на поверхности воды (т.к. пробковый материал легче воды). При этом, поскольку сосуд заполнен водой целиком, при опускании в нее шарика она по з-ну Архимеда частично выплеснется. Сила тяжести, действующая на шарик, равна весу выплеснувшейся воды, так что вес шарика компенсирует ее. Поэтому равновесие весов сохранится.
  2. Масса стального шарика больше, чем масса воды, которую он выплеснет из сосуда, погрузившись в нее. Это означает, сила тяжести больше веса выплеснувшейся воды, и под действием результирующей этих сил равновесие будет нарушено.
  3. Ситуация, при которой в 1-м случае равновесие не нарушается, а во 2-м нарушается, соответствует варианту ответа 2

Ответ: 2

Текст: Базанов Даниил, 6.4k 👀