Задание №6 ЕГЭ по математике профильного уровня

Планиметрия. Углы.

Задание №6 профильного уровня ЕГЭ по математике — решение геометрических задач. В данном задании необходимо справиться с задачей по планиметрии на определение углов.

Теория к заданию №6

Немного стоит напомнить об углах в окружности, так как в задачах это достаточно популярная тематика.

Центральный и вписанный углы:

центральный и вписанный углы

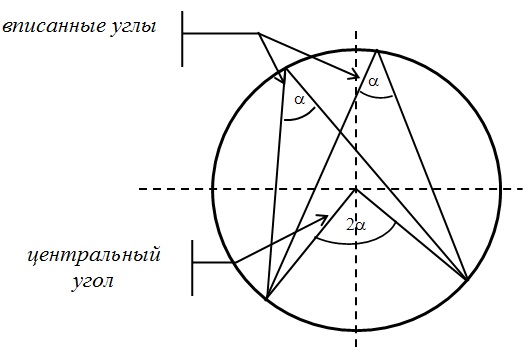
Разбор типовых вариантов заданий №6 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=»#defae6″]

Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC . Ответ дайте в градусах. 

[/su_note]

Алгоритм решения:
  1. Выполняем рисунок.
  2. Определяем вид угла.
  3. Применяем свойство вписанных углов и вычисляем искомый угол.
  4. Записываем ответ.
Решение:

1. Выполняем рисунок.

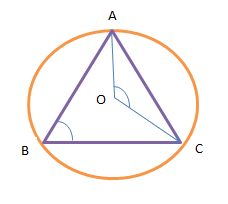
2. Угол, который нужно найти является центральным. Он опирается на ту же дугу, что и угол АВС.

3. Вспомнить правило: «центральный угол в два раза больше вписанного, который опирается на ту же дугу».

4. Вписанный угол АВС, согласно условию, равен 320. Тогда центральный угол BOC равен 320∙ 2 = 640

Ответ: 640.

Второй вариант задания (из Ященко, №1)

[su_note note_color=»#defae6″]

Площадь треугольника ABC равна 152. DE — средняя линия. Найдите площадь треугольника CDE.

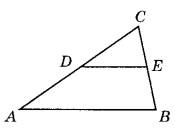
[/su_note]

Алгоритм решения:
  1. Устанавливаем подобие треугольников.
  2. Используем свойство площадей подобных треугольников.
  3. Записываем ответ.
Решение:

1. DE – средняя линия треугольника, следовательно, все стороны в треугольнике CDE меньше соответствующих сторон в треугольнике ABC. Это означает, что треугольники подобны, и коэффициент подобия равен 2.

2. Площади подобных фигур относятся как квадраты коэффициентов подобия, следовательно, площадь треугольника CDE в http://self-edu.ru/htm/math_egecat6/files/3_2.files/image002.gif  раза меньше, чем площадь треугольника ABC. Имеем:

152 / 4 = 38

Ответ: 38.

Третий вариант задания (из Ященко, №23)

[su_note note_color=»#defae6″]

Четырёхугольник ABCD вписан в окружность. Угол ABD равен 36°, угол CAD равен 52°. Найдите угол ABC. Ответ дайте в градусах.

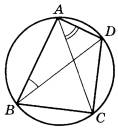
http://self-edu.ru/htm/ege2016_30/files/23_6.files/image001.jpg

[/su_note]

Алгоритм решения:
  1. Отмечаем на рисунке углы, которые ланы в задаче.
  2. Используем свойство вписанных углов.
  3. Находим угол АВС.
  4. Записываем ответ.
Решение:

1. Отмечаем углы ABD и CAD на рисунке. Эти углы вписаны в окружность.

2. Воспользуемся свойством вписанных в окружность углов: они равны градусной меры дуги, на которую опираются.

Тогда угол ABD, опирающийся на дугу AD. Градусная мера ее равна 360∙2=720, второй – угол CAD опирается на дугу CD с градусной мерой 520∙2=1040.

3. Дуга AC=AD+CD. Она имеет градусную меру: АС=720+1040=1760, а угол АВС, который на нее опирается, определяется как половина величины дуги: 1760:2=880.

Ответ: 88.

Четвертый вариант задания (из Ященко, №10)

[su_note note_color=»#defae6″]

Угол АСВ равен 54°. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138°. Найдите угол DAE. Ответ дайте в градусах.

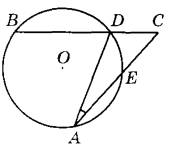
[/su_note]

Алгоритм решения:
  1. Вычисляем угол BDA.
  2. Определяем величину угла ADC,
  3. Рассматриваем треугольник ADC, определяем искомый угол.
  4. Записываем ответ.
Решение:

1. Вычислим угол BDA. Он вписан в окружность, опирается на дугу AB. Тогда по свойству вписанных углов, его градусная мера равна половине градусной величины дуги AB. Тогда http://self-edu.ru/htm/ege2017_36/files/10_6.files/image002.gif .

2. Рассматриваем угол ADC. Он смежный с углом BDA, значит,

3. Рассматриваем треугольник ADC. В нем известны два угла. По свойству суммы углов треугольника третий угол DAC можно найти так:

Из рисунка видно, что угол DAC совпадает с углом DAE, следовательно, угол DAE тоже равен 150.

Ответ: 150.

Текст: Базанов Даниил, 13.1k 👀