Задание №7 ЕГЭ по математике базового уровня

---

Простейшие уравнения

---

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

---

Вариант 7МБ1

[su_note note_color=»#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3)² = x² + 2 · x · 3 + 3² = x² + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — 9)² = x² — 2 · x · 9 + 9² = x² — 18x + 81

После преобразования выражение примет вид:

x² + 6x + 9 = x² — 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 6x — x² + 18x = 81 — 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 6x — x² + 18x = (x² — x²) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 — 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

 

 

 

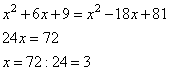
Ответ: 3.

---

Вариант 7МБ2

[su_note note_color=»#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2)² = x² + 2 · x · 2 + 2² = x² + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — 8)² = x² — 2 · x · 8 + 8² = x² — 16x + 64

После преобразования выражение примет вид:

x² + 4x + 4 = x² — 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 4x — x² + 16x = 64 — 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 4x — x² + 16x = (x² — x²) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 — 4

Преобразуем правую часть. 64 — 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

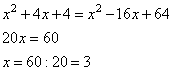
Ответ: 3.

---

Вариант 7МБ3

[su_note note_color=»#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

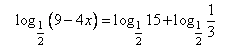
Преобразуем правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).

Выполним преобразование:

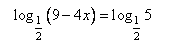
Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

Решим уравнение относительно x.

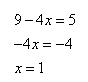
Ответ: 1.

---

Вариант 7МБ4

[su_note note_color=»#defae6″]

Найдите корень уравнения 3^{x− 3} = 81.

[/su_note]

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае — это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором — 9, при третьем — три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

3^{x− 3} = 3⁴

х — 3 = 4

Откуда:

х = 7

Ответ: 7

---

Вариант 7МБ5

[su_note note_color=»#defae6″]

Найдите корень уравнения log₂( x − 3) = 6 .

[/su_note]

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

x − 3 = 2⁶

x − 3 = 64

x = 67

Ответ: 67

---

Вариант 7МБ6

[su_note note_color=»#defae6″]

Найдите отрицательный корень уравнения x² − x − 6 = 0.

[/su_note]

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

D = b² − 4ac

Решение:

D = -(1)² − 4 • 1 • (-6) = 25

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 — 5) : 2 = -2

Так как нам необходим отрицательный корень — ответ -2

Ответ: -2.

---

Вариант 7МБ7

[su_note note_color=»#defae6″]

Решите уравнение х² = –2х + 24.

Если уравнение имеет больше одного корня, в ответе укажите больший из них.

[/su_note]

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

х² = –2х +24

х² +2х – 24 = 0

По т.Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.

Поскольку требуется указать больший из корней, то ответом будет 4.

Ответ: 4

---

Вариант 7МБ8

[su_note note_color=»#defae6″]

Найдите корни уравнения 4^х–6 = 64.

[/su_note]

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

4^х–6 = 64

4^х–6 = 4³

х – 6 = 3

х = 9

Ответ: 9

---

Вариант 7МБ9

[su_note note_color=»#defae6″]

Найдите корень уравнения log₃ (2x – 5) = 2.

[/su_note]

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xyⁿ=nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

log₃ (2x – 5) = 2

log₃ (2x – 5) = 2 · log₃3

log₃ (2x – 5) = log₃3²

2x – 5 = 3²

2x – 5 = 9

2x = 14

x=7

Ответ: 7

---

Вариант 7МБ10

[su_note note_color=»#defae6″]

Найдите корень уравнения

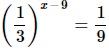
[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)^х=а^–х.
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

–x + 9 = –2

–x = –2–9

x = 11

Ответ: 11

---

Вариант 7МБ11

[su_note note_color=»#defae6″]

Найдите корень уравнения (х – 8)² = (х – 2)².

[/su_note]

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)²=х²–2ху–у².
2. Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
3. Приводим подобные слагаемые. В результате уравнение стало линейным.
4. Решаем полученное уравнение.

Решение:

(х – 8)² = (х – 2)²

х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²

х² – 16х + 64 = х² – 4х + 4

х² – 16х +64 – х² + 4х – 4 = 0

–12х + 60 = 0

–12х = –60

х = 5

Ответ: 5

---

Вариант 7МБ12

[su_note note_color=»#defae6″]

Найдите корень уравнения

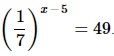
[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)^х=а^–х.
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

–(x–5) = 2

5 – x = 2

–x = 2 – 5

x = 5 – 2

x = 3

Ответ: 3

---

Вариант 7МБ13

[su_note note_color=»#defae6″]

Решите уравнение х² – 25 = 0

[/su_note]

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

х² – 25 = 0

х² = 25

х = ±√25

х₁ = –5, х₂ = 5

Для ответа берем 5.

Ответ: 5

---

Вариант 7МБ14

[su_note note_color=»#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

log₅ (24 – 7x) = log₅ 3

24 – 7x = 3

–7x = 3 – 24

7x = 21

x = 3

Ответ: 3

---

Вариант 7МБ15

[su_note note_color=»#defae6″]

Найдите корень уравнения

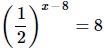
[/su_note]

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)^х=а^–х.
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

2^–(x–8) = 2³

–x+8 = 3

–x = 3–8

x = 5

Ответ: 5

---

Вариант 7МБ16

[su_note note_color=»#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. К левой части уравнения применяем св-во логарифмов log_a(x/y)=log_ax–log_ay.
2. Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
3. Решаем его.

Решение:

log₃ (2x + 4) – log₃ 2 = log₃ 5

log₃ (2x + 4)/2 = log₃ 5

log₃ (x + 2) = log₃ 5

x + 2 = 5

x = 3

Ответ: 3