Механические явления
Задание № 7 является комплексным, предполагающим использование любого раздела механики. В нем может потребоваться знание основных понятий как кинематики (ср.скорость, ускорение, перемещение), так и динамики (силы в природе, з-ны Ньютона), аэро- и гидродинамики, статики. Часть полезной информации рассмотрена в теоретическом разделе к заданию № 7. Это определения и формулы, которые не были необходимы для решения прочих заданий из курса механики. Большинство же теоретических сведений рассмотрены в разделах теории к другим заданиям по соответствующим темам.
Теория к заданию №7 ОГЭ по физике
Динамометр
Динамометром называют устройство для количественного измерения силы. Это прибор, состоящей из силового звена, содержащего упругий элемент, и шкалы с делениями в ньютонах или дольных (либо кратных) значениях этой единицы измерения. Простейший динамометр действует с использованием обычной пружины соответствующей жесткости.
С помощью динамометра может быть измерен еще и момент силы.
КПД
КПД – коэффициент полезного действия – показатель эффективности системы, осуществляющей преобразование и (или) передачу энергии. Системой в данном случае может выступать устройство, механизм и т.п. КПД в физике принято обозначать греческой буквой ɳ («эта»).
Вычисляется КПД по формулам:
![]()
где Еп, Ап, Nп – соответственно полезная энергия, работа, мощность; Е, А, N – полная (затраченная) энергия, работа, мощность.
Разбор типовых вариантов заданий №7 ОГЭ по физике
Демонстрационный вариант 2018
[su_note note_color=»#defae6″]
К динамометру прикрепили цилиндр, как показано на рисунке 1. Затем цилиндр полностью погрузили в воду (рисунок 2).
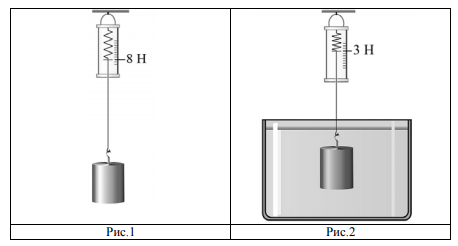
Определите объём цилиндра.
Ответ: _____ см3.
[/su_note]
Алгоритм решения:
- Записываем табличное значение для плотности воды, которое понадобится при решении.
- Анализируем условие и рис.1. Определяем силы, действующие в этом случае на цилиндр. Составляем уравнение для равнодействующей, т.е. для состояния равновесия цилиндра (1).
- Анализируем рис.2. Определяем силы, действующие на цилиндр после погружения. Выводим уравнение для равнодействующей (2). Подставляем (1) в (2), получаем уравнение для выталкивающей силы (3).
- Записываем формулу для силы Архимеда (4). Объединив (4) и (3), получаем уравнение для искомого объема. Вычисляем его.
Решение:
- Плотность воды составляет:
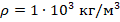 .
. - До погружения в воду на цилиндр действует сила тяжести (mg, направленная вертикально вниз) и сила натяжения нити динамометра F1 (направленная вверх), значение которого отражает динамометр на рис.1. Поскольку цилиндр достиг состояния равновесия, то
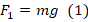 .
. - После погружения в воду на цилиндр действует еще и выталкивающая – архимедова – сила (FA). Именно поэтому значение динамометра (F2) изменилось:
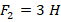 . При этом для состояния равновесия получаем:
. При этом для состояния равновесия получаем: 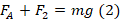 .
. 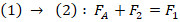 . Отсюда:
. Отсюда: 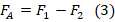
- Выталкивающая сила равна:
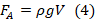 . Поскольку на рисунке показано, что цилиндр погрузился в воду целиком, то V в данном случае – объем всего тела, что и является искомой величиной. (3=4):
. Поскольку на рисунке показано, что цилиндр погрузился в воду целиком, то V в данном случае – объем всего тела, что и является искомой величиной. (3=4): 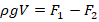 . Выражаем объем:
. Выражаем объем: 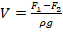 . Тогда:
. Тогда: 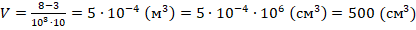 .
.
Ответ: 500 см3.
Первый вариант (Камзеева, № 5)
[su_note note_color=»#defae6″]
Под действием силы 20 Н груз массой 2 кг перемещается вверх по наклонной плоскости (трение пренебрежимо мало). Коэффициент полезного действия наклонной плоскости 50%. Чему равна длина наклонной плоскости, если ее высота 1 м?
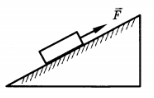
Ответ: ____м
[/su_note]
Алгоритм решения:
- Записываем формулу для нахождения КПД с использованием работы (1).
- Выражаем из нее уравнение для нахождения полезной работы (2).
- Записываем уравнение для полной работы (3).
- Находим значение для КПД, подставив (2) и (3) в (1). Из него выражаем искомую длину.
Решение:
- КПД в данном случае может быть найден по формуле:
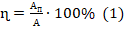 . При этом полезной является работа, выполненная для подъема груза на заданную высоту (h = 1 м).
. При этом полезной является работа, выполненная для подъема груза на заданную высоту (h = 1 м). - Поскольку A = F • S , то полезная работа, выполненная для поднятия тела на высоту, заключается в преодолении силы тяжести. При этом s = h . Тогда получаем:
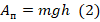 .
. - Полная работа равна A = F • l (3), поскольку для того, чтобы поднять груз на высоту h, требуется преодолеть расстояние l.
- (2,3) → (1) :
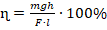 . Отсюда:
. Отсюда: 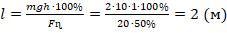
Ответ: 2 метра.
Второй вариант (Камзеева, № 8)
[su_note note_color=»#defae6″]
Под действием тормозящей силы в 100 кН тормозной путь поезда массой 100 т составил 50 м. Какую скорость имел поезд до начала торможения?
Ответ: ___ м/с
[/su_note]
Алгоритм решения:
- Переводим в СИ несоответствующие ей значения величин.
- Записываем уравнение 2-го закона Ньютона. Находим из него ускорение. Вычисляем его значение.
- Записываем формулу для перемещения при равнозамедленном движении. Из нее выражаем искомую скорость. Вычисляем ее.
Решение:
- Записываем значения в СИ: тормозящая сила
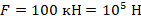 ; масса
; масса 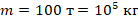 .
. - По 2-му закону Ньютона
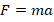 . Отсюда:
. Отсюда: 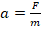 . Найдем величину ускорения:
. Найдем величину ускорения: 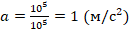 .
. - Поскольку в условии не дано время, используем для расчета скорости формулу
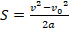 . Здесь: 1) v – конечная скорость, которой в данном случае является скорость после завершения торможения (значит, v=0); 2) v0 – скорость перед началом торможения, т.е. искомая скорость; 3) а<0, т.к. при торможении вектор перемещения и ускорения направлены противоположно. Тогда получим:
. Здесь: 1) v – конечная скорость, которой в данном случае является скорость после завершения торможения (значит, v=0); 2) v0 – скорость перед началом торможения, т.е. искомая скорость; 3) а<0, т.к. при торможении вектор перемещения и ускорения направлены противоположно. Тогда получим: 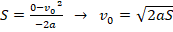 Определяем скорость:
Определяем скорость: 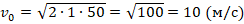 .
.
Ответ: 10 м/с
Третий вариант (Камзеева, № 13)
[su_note note_color=»#defae6″]
Движущийся шар массой 4 кг соударяется с неподвижным шаром массой 2 кг. После удара шары движутся как единое целое со скоростью 2 м/с. Чему была равна скорость первого шара до соударения?
Ответ: ___ м/с
[/su_note]
Алгоритм решения:
- Вводим обозначения для необходимых для решения физ.величин.
- Анализируем ситуацию до удара шаров и после него.
- Используя уравнение закона сохранения импульса, найдем искомую скорость.
Решение:
- Обозначим для 1-го (движущегося) шара массу и скорость соответственно m1 и v1. Аналогично для 2-го (неподвижного) шара – m2 и v2. Скорость после соударения обозначим v’.
- До удара 1-й шар имеет некую ненулевую скорость, которая и является искомой величиной. 2-й шар имеет
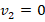 . После соударения шары двигаются вместе, т.е. имеют одинаковую скорость. Поэтому
. После соударения шары двигаются вместе, т.е. имеют одинаковую скорость. Поэтому 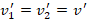 . Поскольку шары после удара непосредственно контактируют друг с другом, то их система представляет собой единой физ.тело с массой (
. Поскольку шары после удара непосредственно контактируют друг с другом, то их система представляет собой единой физ.тело с массой ( 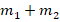 ).
). - По з-ну сохранения импульса
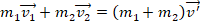 . Здесь векторы v1 и v’ сонаправлены, вектор v2 нулевой (т.к. по условию до удара 2-й шар неподвижен). Тогда получим:
. Здесь векторы v1 и v’ сонаправлены, вектор v2 нулевой (т.к. по условию до удара 2-й шар неподвижен). Тогда получим: 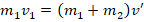 . Отсюда
. Отсюда 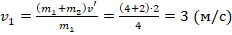 .
.
Ответ: 3 м/с