Задание №8 ЕГЭ по математике профильного уровня

---

Стереометрия

---

Задание №8 в профильном уровне ЕГЭ по математике проверяет базовые знания стереометрии. Задания в этом разделе простые, на базовые формулы — обычно на объемы простых стандартных фигур — цилиндра, куба, пирамиды, конуса.

---

Теория к заданию №8

---

Приведу формулы объема фигур, так данный материал довольно часто встречается.

---

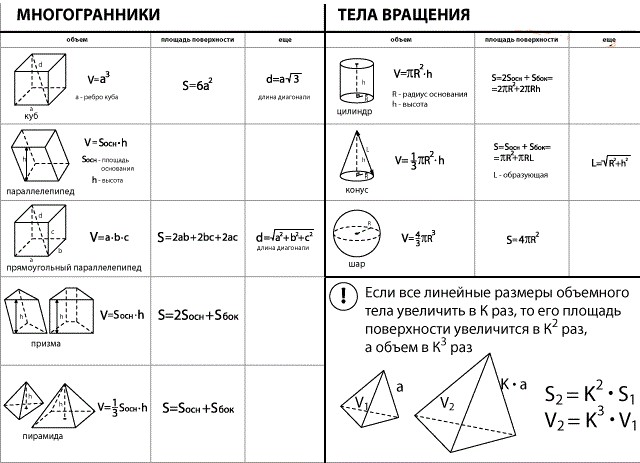
Разбор типовых вариантов заданий №8 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=»#defae6″]

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.

[/su_note]

Алгоритм решения:

1. Определяем площадь основания первого и второго сосудов.
2. Записываем формулы объемов и приравниваем их.
3. Убираем одинаковые величины. Делаем вывод.
4. Записываем ответ.

Решение:

1. Площадь основания первого сосуда определяется формулой

Диаметр второго сосуда в 2 раза больше. Значит площадь основания его равна

то есть в 4 раза больше:

2 Записываем формулы объема жидкости в каждом сосуде.

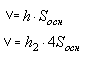
Так как объем жидкости остается постоянным, получаем уравнение:

Убираем одинаковые величины. Отсюда

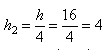
Ответ: 4.

---

Второй вариант задания (из Ященко, №1)

[su_note note_color=»#defae6″]

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.

[/su_note]

Алгоритм решения:

1. Записываем формулу объема конуса.
2. Записываем формулу объема цилиндра.
3. Сравниваем формулы, делаем вывод.
4. Вычисляем объем цилиндра.
5. Записываем ответ.

Решение:

1. Объем конуса определяем по формуле

где H – высота конуса; R – радиус основания конуса.

2. Объем цилиндра определяем по формуле

3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.

4. Вычисляем объем цилиндра::

Ответ: 84.

---

Третий вариант задания (из Ященко)

[su_note note_color=»#defae6″]

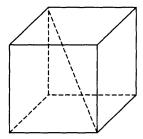
Диагональ куба равна . Найдите его объём.

[/su_note]

Алгоритм решения:

1. Выражаем диагональ куба, используя теорему Пифагора.
2. Решаем полученное уравнение.
3. Вычисляем объем.
4. Записываем ответ.

Решение:

1. По тереме Пифагора диагональ грани куба определяется формулой:

Тогда диагональ куба

2. Отсюда

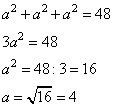
3. Объем куба равен

Ответ: 64.