Задание №9 ЕГЭ по математике профильного уровня

Преобразования и вычисления

В задании №9 ЕГЭ по математике профильного уровня нам необходимо выполнить преобразование выражений и произвести элементарные вычисления. Чаще всего в этом разделе встречаются тригонометрические выражения, поэтому для успешного выполнения необходимо знать формулы приведения и другие тригонометрические тождества.

Разбор типовых вариантов заданий №9 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=»#defae6″]

Найдите sin2α , если cosα = 0,6 и π < α < 2π.

[/su_note]

Алгоритм решения:
  1. Находим значение синуса данного угла.
  2. Вычисляем значение sin2α.
  3. Записываем ответ.
Решение:

1. α лежит в третьей или четвертой четвертях, значит синус угла отрицательный. Воспользуемся осномным тригонометрическим тождеством:

http://vopvet.ru/gdz/2015-08-28_145749.png

2. По формуле синуса двойного угла: sin2α = 2sinαcosα = 2∙(-0,8)∙0,6 = -0,96

Ответ: -0,96.

Второй вариант задания (из Ященко, №1)

[su_note note_color=»#defae6″]

Найдите , если .

[/su_note]

Алгоритм решения:
  1. Преобразуем формулу косинуса двойного угла.
  2. Вычисляем косинус.
  3. Записываем ответ.
Решение:

1. Преобразуем формулу косинуса двойного угла:

2. Вычисляем косинус искомого угла 2α, умноженный на 25, подставив данное значение косинуса угла α

Ответ: -7.

Третий вариант задания (из Ященко, №16)

[su_note note_color=»#defae6″]

Найдите значение выражения http://self-edu.ru/htm/ege2016_36/files/10_9.files/image001.gif .

[/su_note]

Алгоритм решения:
  1. Рассматриваем выражение.
  2. Используем свойства тригонометрических функций для определения значений синуса и косинуса заданных углов.
  3. Вычисляем значение выражения.
  4. Записываем ответ.
Решение:

1. Выражение представляет собой произведение чисел и значений тригонометрических функций отрицательных углов.

2. Воспользуемся формулами:

3. Тогда получаем:

Ответ: -23.

Четвертый вариант задания (из Ященко)

[su_note note_color=»#defae6″]

Найдите значение выражения 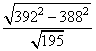http://self-edu.ru/htm/ege2016_36/files/29_9.files/image001.gif.

[/su_note]

Алгоритм решения:
  1. Анализируем выражение.
  2. Преобразовываем и вычисляем выражение.
  3. Записываем ответ.
Решение:

1. Выражение содержит два корня. Под корнем в числителе стоит разность квадратов. Для упрощения вычислений можно разность квадратов разложить на множители по формуле сокращенного умножения.

2. Преобразовываем выражение и вычисляем его значение:

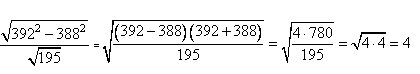
Ответ: 4.

Пятый вариант задания (из Ященко)

[su_note note_color=»#defae6″]
Найдите значение выражения .
[/su_note]

Алгоритм решения:
  1. Анализируем выражение.
  2. Преобразовываем и вычисляем выражение.
  3. Записываем ответ.
Решение:

1. Данное выражение представляет собой произведение множителей, которые можно по формулам сокращенного умножения записать в виде разности квадратов:

2. Имеем:

Ответ: -5.

Текст: Базанов Даниил, 11.5k 👀