Задание 15МО09 (теплицы)
Виктор Николаевич решил построить на дачном участке теплицу длиной 6 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы он заказал металлические дуги в форме полуокружности длиной 5 метров каждая, а также покрытие для обтяжки.
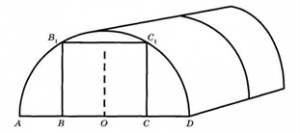
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется сделать вход, который показан на рисунке прямоугольником ВВ1С1С, где точки В,О и С делят отрезок АД на равные части.
Внутри теплицы Виктор Николаевич планирует сделать три грядки по длине теплицы – одну центральную широкую и две по узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых нужно купить тротуарную плитку размером 25 см 25 см.
📜Теория для решения:
Посмотреть решение
Задание №1. Какое наименьшее количество дуг надо заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение
На рисунке дуги выделены красным цветом и показано, что расстояние между ними не более 80 см.
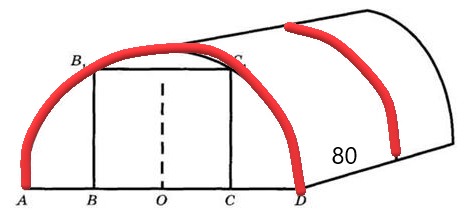
Зная, что длина теплицы 6 метров, переведем её в сантиметры: 6м=600 см. Теперь разделим 600 см на 80 см, получим 7,5. Округлим до целого числа и получим 8, но это не количество дуг, а количество расстояний (отрезков) между ними. Далее нужно прибавить единицу, чтобы получить точное количество: 8+1=9 дуг.
Если способ с рисунком теплицы не совсем понятен, то можно изобразить дуги точками на отрезке вот таким образом.

Ответ: 9
Задание №2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение
По условию задачи знаем, что в теплице будет три грядки, следовательно, будет две дорожки, ширина которых по условию 50 см. Длина каждой дорожки равна длине теплицы, т.е. 600 см.
Зная длину и ширину дорожки, можно найти её площадь: 600×50=30000 см2. Таких дорожек у нас две, значит 30000×2=60000 см2.
По условию задачи известно, что тротуарная плитка имеет размеры 25 см ×25 см. Можно найти площадь одной плитки: 25 см ×25 см=625 см2.
Теперь находим количество плиток для двух дорожек: 60000:625=96 плиток.
Так как сказано, что плитки продаются в упаковках по 10 штук, то разделим 96 на 10, получим 9,6. Необходимо округлить результат до целого числа, так как отдельно несколько плиток нам не продадут, поэтому 9,6≈10.
Ответ: 10
Задание №3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение
Ширина теплицы – это диаметр полуокружности. По условию задачи Виктор Николаевич покупал дуги длиной 5 метров, значит, длина полуокружности и есть 5 метров.
Вспомним формулу, которая связывает длину окружности и радиус: С=2πR, также можно воспользоваться и формулой С=πd, так как нам надо найти ширину теплицы, т.е. диаметр.
Подставим значения в формулу, помня о том, что полная длина окружности будет равна 10 м: 10=3,14d. Отсюда d=10:3,14=3,184…≈3,2 (так как по условию требуется округлить до десятых).
Ответ: 3,2
Задание №4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение
Покажем на рисунке, как выглядят грядки и дорожки внутри теплицы, расставим известные данные: 50 см – по условию, а 320 см – из решения задания №3.
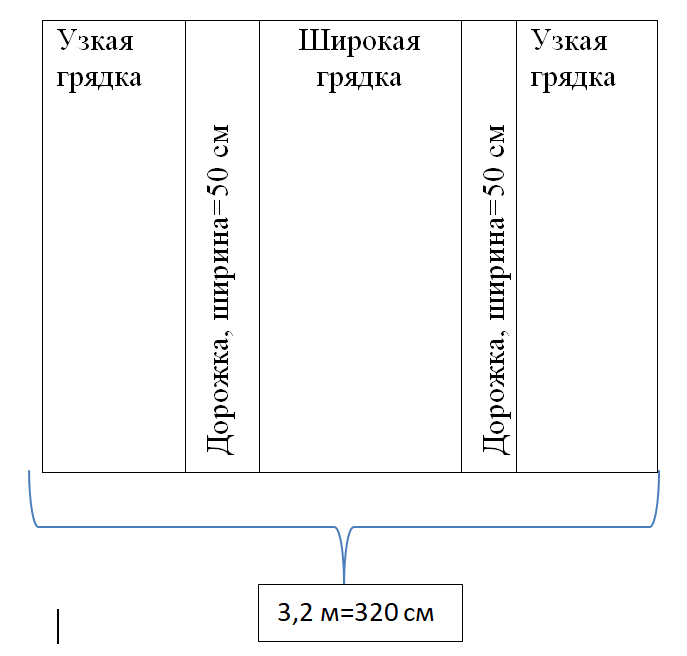
Для удобства решения определим ширину всех грядок вместе, то есть уберем ширину дорожек: 320-50-50=220 см.
По условию задачи ширина центральной грядки относится к ширине узкой грядки как 5:3, т.е. можно сказать, что на центральную грядку (широкую) приходится 5 частей, а на крайние грядки (узкие) по 3 части. Значит, всего на три грядки приходится 3+5+3=11 равных частей. Так как вся ширина грядок 220 см, то 220:11=20 см ширина одной части. Значит, ширина узкой грядки будет равна 20 см×3=60 см.
Ответ: 60 см
Задание №5. Сколько квадратных метров пленки необходимо купить для передней и задней стенок теплицы, если с учетом крепежа ее нужно брать с запасом 15%? Ответ округлить до десятых.
Решение
Передняя и задняя стенки теплицы являются полукругами одинакового диаметра, следовательно, два полукруга вместе – это круг, диаметр которого (ширина теплицы) мы нашли в задаче №3, т.е.3,2 метра. Площадь круга находится по формуле S=πR2. Зная, что диаметр равен 3,2 м, найдем радиус: 3,2:2=1,6 м. Подставим в формулу данные и найдем площадь круга: S=3,14×1,62=8,0384 м2
По условию задачи сказано, что с учетом крепежа пленку надо покупать с запасом 15%. Найдем 15% от данного числа, переведя 15% в десятичную дробь: 0,15×8,0384=1,20576.
Теперь складываем площадь круга и найденные 15%: 8,0384+1,20576=9,24416.
Так как ответ надо округлить до десятых, то получим: 9,24416≈9,2
Ответ: 9,2
Ответ: см. решение