Задание EF22574 • СПАДИЛО

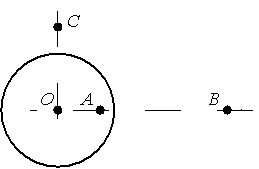На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?

Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

📜Теория для решения: Электростатическое поле точечного заряда и заряженной сферы

Посмотреть решение

Алгоритм решения

1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.

2.Определить величину напряженности поля в указанных точках.

3.Установить соответствие между величинами и их значениями.

Решение

Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.

$E_{A} = 0$

Снаружи заряженной сферы напряженность электростатического поля равна:

$E = \frac{k Q}{r^{2}} = \frac{k Q}{{(R + a)}^{2}}$

Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:

$E_{B} = \frac{k Q}{r^{2}} = \frac{k Q}{{(3 R)}^{2}} = \frac{k Q}{{9 R}^{2}}$

Чтобы выразить $E_{B}$ через $E_{с}$ , найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:

$E_{С} = \frac{k Q}{r^{2}} = \frac{k Q}{{(\frac{3}{2} R)}^{2}} = \frac{4 k Q}{{9 R}^{2}}$

Найдем отношение $E_{B}$ к $E_{с}$ :

$\frac{E_{B}}{E_{С}} = \frac{k Q}{{9 R}^{2}} \div \frac{4 k Q}{{9 R}^{2}} = \frac{k Q}{{9 R}^{2}} \cdot \frac{{9 R}^{2}}{4 k Q} = \frac{1}{4}$

Следовательно:

$E_{B} = \frac{E_{С}}{4}$

Ответ: 14

Текст: Алиса Никитина, 882 👀