Прикладные задачи
Задание 10 профильного уровня в ЕГЭ по математике проверяет наши математические знания в прикладных аспектах. Сами по себе математически задания несложные, но они завуалированы под задачи из реальной жизни. В ОГЭ по математике они входят в раздел реальная математика. Так как в ЕГЭ разделов напрямую нет, то данной тематике посвятили задание №10. Как таковой теории в данном разделе нет, обычно необходимо выразить неизвестное из формулы и подставить известные значения. Что же, давайте рассмотрим пару вариантов!
Разбор типовых вариантов заданий №10 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=»#defae6″]
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
![]()
где = 1500 м/с — скорость звука в воде,f0 — частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала, если батискаф погружается со скоростью 2 м/с.
[/su_note]
Алгоритм решения:
- Анализируем равенство, связывающее частоту сигнала, скорость звука в воде и остальные заданные величины.
- Подставляем заданные числовые значения величин, составляющих равенство, преобразовываем его.
- Вычисляем частоту отраженного сигнала.
- Записываем ответ.
Решение:
1. Потому как скорость погружения батискафа равна 2 м/с, то для определения частоты f достаточно решить уравнение v=2.
2. Подставляем в заданное для решения задачи выражение известные величины и решаем уравнение:
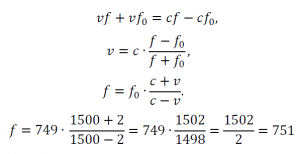
Значит, регистрируемая батискафом частота отражающегося сигнала, равна 751 МГц.
Ответ: 751.
Второй вариант задания (из Ященко)
[su_note note_color=»#defae6″]
В розетку электросети подключены приборы, общее сопротивление которых составляет R1=56 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление задаётся формулой ![]() , а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 24 Ом. Ответ дайте в омах.
, а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 24 Ом. Ответ дайте в омах.
[/su_note]
Алгоритм решения:
- Анализируем равенствов, связывающее частоту сопротивления
- Подставляем известные значения и преобразовываем равенство.
- Выполняем преобразования и находим ответ на поставленный вопрос.
- Записываем ответ.
Решение:
1. В задаче дана величина сопротивления R1=56 Ом. Требуется подобрать минимальное значение R2, такое, что дает сопротивление сети равное 24 Ом.
2. Поскольку формула для вычисления дана, подставляя в нее заданные значения величин, имеем:
![]()
3. Решаем полученное уравнение:

Получаем, что искомое сопротивление R2 равно 42 Ом.
Ответ: 42.
Третий вариант задания (из Ященко)
[su_note note_color=»#defae6″]
Водолазный колокол, содержащий в начальный момент времени v = 2 моля воздуха объёмом V1=10л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V2. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле ![]() , где
, где ![]() — постоянная, а Т = 300 К — температура воздуха. Найдите, какой объём V2 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 15 960 Дж.
— постоянная, а Т = 300 К — температура воздуха. Найдите, какой объём V2 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 15 960 Дж.
[/su_note]
Алгоритм решения:
- Анализируем выражение, связывающее заданные величины с искомой,
- Преобразовываем равенство.
- Подставляем известные значении величин.
- Вычисляем и отвечаем на поставленный вопрос.
- Записываем ответ.
Решение:
1. В выражении, связывающем работу с объемом, присутствует логарифм. При преобразовании выражения придется использовать свойства логарифмов.
2. Выразим объем V2 воздуха, который он займет после выполнения работы А=15960 Дж по его сжатию:
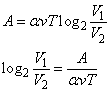
Выражаем дробь, стоящую под логарифмом:
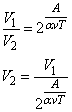
3. Подставляем числа вместо величин ![]() :
:
![]()
4. Вычисляем требуемое значение объема.
![]()
Ответ: 2,5.