Выбор оптимального варианта
В задании №12 базового уровня ЕГЭ по математике нам необходимо выбрать оптимальный вариант из нескольких предложенных, предварительно совершив несложные математические операции. Опять же, поскольку данное задание относится к разделу реальной математики, то какой-либо теории здесь нет, а есть только подходы к решениям, которые я изложил ниже в разборе типовых вариантов.
Разбор типовых вариантов заданий №12 ЕГЭ по математике базового уровня
Вариант 12МБ1
[su_note note_color=»#defae6″]
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
| Номер переводчика | Язык | Стоимость услуг(руб. в день) |
| 1 | Немецкий, испанский | 7 000 |
| 2 | Английский, немецкий | 6 000 |
| 3 | Английский | 3 000 |
| 4 | Английский, французский | 6 000 |
| 5 | Французский | 2 000 |
| 6 | Испанский | 4 000 |
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения:
- Выбрать язык, которым владеют наименьшее количество переводчиков.
- Дополнить недостающими языками, следя за стоимостью услуг.
Решение:
Выберем язык, которым владеют наименьшее количество переводчиков.
Немецким владеют два переводчика 1 и 2. Возьмем 2, так как стоимость его услуг ниже, а бюджет ограничен.
Дополним недостающими языками, следя за стоимостью услуг.
Остались испанский и французский. Переводчики 5 и 6 владеют испанским и французским. Проверим суммарную стоимость услуг переводчиков.
6 000 + 2 000 + 4 000 = 12 000.
Такая группа подходит по условию задания.
Ответ: 256
Примечание: Приведенное решение является лишь одним из многих. То есть по сути задание решается подбором групп и проверкой суммарной стоимости.
Вариант 12МБ2
[su_note note_color=»#defae6″]
В таблице приведены данные о шести сумках.
| Номер сумки | Длина (см) | Высота (см) | Ширина (см) | Масса (кг) |
| 1 | 49 | 31 | 25 | 10,7 |
| 2 | 62 | 47 | 20 | 5,9 |
| 3 | 45 | 37 | 18 | 8,7 |
| 4 | 46 | 35 | 15 | 6,4 |
| 5 | 59 | 40 | 18 | 7,5 |
| 6 | 50 | 40 | 20 | 12,4 |
По правилам авиакомпании в ручную кладь может быть взята сумка, сумма трёх измерений (длина, высота, ширина) которой не должна превышать 115 см, а масса не должна быть больше 10 кг. Какие сумки можно взять в ручную кладь по правилам этой авиакомпании?
В ответе укажите номера выбранных сумок без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения:
- Выбрать все сумки, масса которых меньше 10 кг.
- Вычислить сумму трех измерений оставшихся сумок.
- Выбрать из полученных значений те, что не превышают 115 см.
Решение:
В этом задании нужно выбрать все сумки, масса которых не больше 10 кг и сумма габаритных размеров не превышает 115 см. Выберем все сумки, масса которых меньше 10 кг. Сразу можно отбросить сумки под номерами 1 и 6, т.к. их масса больше 10 кг.
Вычислим сумму трех измерений оставшихся сумок.
— для 2-й: 62+47+20 = 129 см;
— для 3-й: 45+37+18 = 100 см;
— для 4-й: 46+35+15 = 96 см;
— для 5-й: 59+40+18 = 117 см.
Выберем из полученных значений те, что не превышают 115 см.
Под заявленное условие подходят сумки под номерами 3 и 4.
Ответ: 34.
Вариант 12МБ3
[su_note note_color=»#defae6″]
В таблице приведены данные о шести сумках.
| Номер | Длина | Высота | Ширина | Масса |
| сумки | (см) | (см) | (см) | (кг) |
| 1 | 60 | 48 | 15 | 7,6 |
| 2 | 58 | 38 | 13 | 9,8 |
| 3 | 55 | 42 | 23 | 6,8 |
| 4 | 65 | 35 | 15 | 11,3 |
| 5 | 57 | 34 | 21 | 9,6 |
| 6 | 62 | 40 | 10 | 10,5 |
По правилам авиакомпании в ручную кладь может быть взята сумка, сумма трёх измерений (длина, высота, ширина) которой не должна превышать 115 см, а масса не должна быть больше 10 кг. Какие сумки можно взять в ручную кладь по правилам этой авиакомпании?
В ответе укажите номера выбранных сумок без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения:
- Выбрать все сумки, масса которых меньше 10 кг.
- Вычислить сумму трех измерений оставшихся сумок.
- Выбрать из полученных значений те, что не превышают 115 см.
Решение:
В этом задании нужно выбрать все сумки, масса которых не больше 10 кг и сумма габаритных размеров не превышает 115 см. Выберем все сумки, масса которых меньше 10 кг. Сразу можно отбросить сумки под номерами 4 и 6, т.к. их масса больше 10 кг.
Вычислим сумму трех измерений оставшихся сумок.
— для 1-й сумки: 60+48+15 = 123 см;
— для 2-й сумки: 58+38+13 = 109 см;
— для 3-й сумки: 55+42+23 = 130 см;
— для 5-й сумки: 57+34+21 = 112 см.
Выберем из полученных значений те, что не превышают 115 см.
Под заявленное условие подходят сумки под номерами 2 и 5.
Ответ: 25.
Вариант 12МБ4
[su_note note_color=»#defae6″]
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определённой модели. В таблице показано 6 предложений от разных интернет-магазинов.
| Номер магазина | Рейтинг магазина | Стоимость товара (руб.) | Стоимость доставки (руб.) |
| 1 | 3 | 13 895 | 400 |
| 2 | 5 | 18 490 | 0 |
| 3 | 5 | 13 513 | 0 |
| 4 | 5 | 13 745 | 390 |
| 5 | 4 | 13 411 | 399 |
| 6 | 4 | 17 489 | 0 |
Сергей Петрович считает, что покупку нужно делать в магазине, рейтинг которого не ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой низкой стоимостью покупки с учётом доставки. В ответе запишите номер выбранного магазина.
[/su_note]
Алгоритм выполнения:
- Выбрать варианты с рейтингом не ниже 4.
- Вычислить суммарную стоимость товара и доставки для оставшихся интернет-магазинов.
- Выбрать, исходя из полученных результатов, товар с наименьшей стоимостью.
Решение:
Выберем варианты с рейтингом не ниже 4. Это магазины под номерами 2, 3, 4, 5 и 6.
Вычислим суммарную стоимость товара и доставки для оставшихся интернет-магазинов.
2-й магазин: 18490 рублей;
3-й магазин: 13513 рублей;
4-й магазин: 13745+390 = 14 135 рублей;
5-й магазин: 13411+399 = 13 810 рублей;
6-й магазин: 17489 рублей.
Выберем, исходя из полученных результатов, товар с наименьшей стоимостью.
Из вычислений видно, что наименьшую цену предоставляет магазин под номером 3.
Ответ: 3.
Вариант 12МБ5
[su_note note_color=»#defae6″]
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определённой модели. В таблице показано 6 предложений от разных интернет-магазинов.
| Номер магазина | Рейтинг магазина | Стоимость товара (руб.) | Стоимость доставки (руб.) |
| 1 | 4 | 13 790 | 500 |
| 2 | 4 | 16 295 | 500 |
| 3 | 5 | 14 411 | 450 |
| 4 | 3 | 14 463 | 500 |
| 5 | 3,5 | 16 249 | 510 |
| 6 | 4 | 16 900 | 650 |
Сергей Петрович считает, что покупку нужно делать в магазине, рейтинг которого не ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой низкой стоимостью покупки с учётом доставки. В ответе запишите номер выбранного магазина.
[/su_note]
Алгоритм выполнения:
- Выбрать варианты с рейтингом не ниже 4.
- Вычислить суммарную стоимость товара и доставки для оставшихся интернет-магазинов.
- Выбрать, исходя из полученных результатов, товар с наименьшей стоимостью.
Решение:
Выберем варианты с рейтингом не ниже 4. Это магазины под номерами 1, 2, 3 и 6.
Вычислим суммарную стоимость товара и доставки для оставшихся интернет-магазинов.
1-й магазин: 13 790+500 = 14290 рублей;
2-й магазин: 16 295+500 = 16795 рублей;
3-й магазин: 14 411+450 = 14861 рублей;
6-й магазин: 16 900+650 = 17 550 рублей.
Выберем, исходя из полученных результатов, товар с наименьшей стоимостью.
Из вычислений видно, что наименьшую цену предоставляет магазин под номером 1.
Ответ: 1.
Вариант 12МБ6
[su_note note_color=»#defae6″]
Турист подбирает себе экскурсии. Сведения об экскурсиях представлены в таблице.
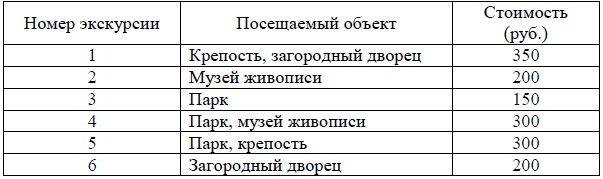
Пользуясь таблицей, подберите экскурсии так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей.
В ответ укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
[/su_note]
Возьмем первую строчку — крепость и загородный дворец у нас есть и мы отдаем за них 350 рублей, нам осталось найти парк и музей живописи. Возьмем вторую и третью строчки — так мы потратим 200 и 150 рублей, а суммарно 700 рублей — это нам не подходит. Заметим четвертую строчку — нам предлагают посетить парк и музей живописи за 300 рублей. Итого с первой строчкой — 650 рублей — это нам подходит!
Ответ: 14.
Вариант 12МБ7
[su_note note_color=»#defae6″]
Строительная фирма планирует купить 70 м3 пеноблоков у одного их трех поставщиков. Цены и условия доставки приведены в таблице.
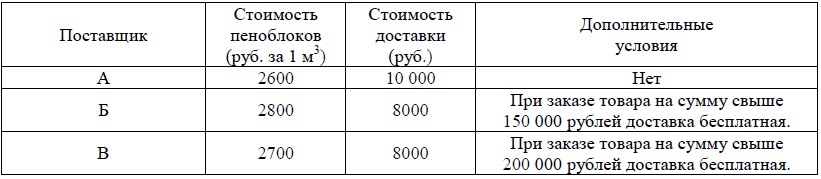
Сколько рублей нужно заплатить за самую дешевую покупку с доставкой?
[/su_note]
Довольно типичная задача. В данном случае просчитать необходимо каждый вариант и выбрать наименьший по стоимости.
В данном случае в ответе необходимо написать сумму, а не номер варианта, будьте внимательны!
Рассмотрим вариант А:
2600 • 70 + 10000 = 182000 + 10000 = 192000
Вариант Б:
2800 • 70 = 196000 — доставка бесплатная, так как сумма заказа больше 150000 рублей
План С:
2700 • 70 = 189000 — доставка платная, так как сумма меньше 200000, итого 197000
Сравнивая все варианты, находим, что наименьший по стоимости — это вариант №1, то есть А, в котором сумма равна 192000.
Ответ: 192000.
Вариант 12МБ8
[su_note note_color=»#defae6″]
В городском парке имеется пять аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Веселый тир». В кассах продается шесть видов билетов, каждый из которых позволяет посетить один или два аттракциона. Сведения о стоимости билетов представлены в таблице.
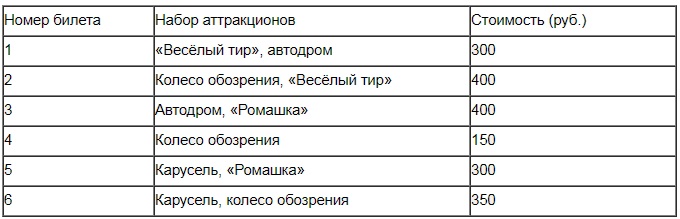
Какие билеты должен купить Андрей, чтобы посетить все пять аттракционов и затратить не более 750 рублей?
В ответе укажите какой-нибудь один набор номеров без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения
- Поскольку требуется посетить 5 аттракционов, то необходимо выбрать 2 набора по 2 аттракциона и один, в котором содержится 1 аттракцион.
- Пары аттракционов должны быть выбраны такие, чтобы их наименования не повторялись.
- Чем меньше стоимость набора, тем больше вероятность уложиться в итоговую сумму в 750 руб.
Решение:
1 аттракцион содержится только в 4-м наборе, поэтому его нужно использовать. Он предполагает посещение колеса обозрения, и на него придется истратить 150 руб.
Использовать 2-й и 3-й наборы нельзя, т.к. сумма 400 руб., 150 руб. (за 4-й набор) и любого другого из оставшихся будет большей, чем 750 руб. Проверяем:
750–(400+150)=200 руб., а набора с такой стоимостью в перечне нет.
Аналогично исключаем 6-й набор, т.к. 750–(350+150)=250 руб., а этой суммы тоже недостаточно, чтобы приобрести еще один набор из оставшихся.
Соответственно, подходящими являются два набора – 1-й и 5-й. Выбрав их, получаем:
150+2·300=750 руб.
Проверяем наборы по содержанию:
- 1-й набор: «Веселый тир», автодром
- 4-й набор: колесо обозрения
- 5-й набор: карусель, «Ромашка»
Т.е. видим, что аттракционы не повторяются.
Ответ: 145
Вариант 12МБ9
[su_note note_color=»#defae6″]
Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трех поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
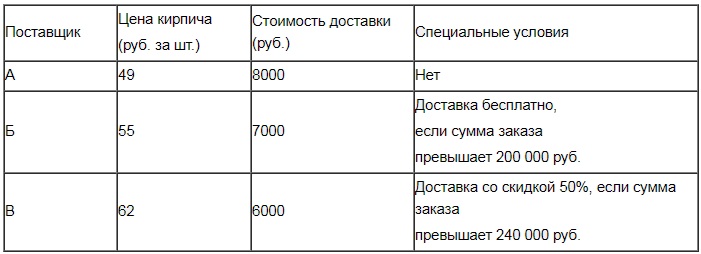
Во сколько рублей обойдется наиболее дешевый вариант покупки с доставкой?
[/su_note]
Алгоритм выполнения
- 20 тонн переводим в кг.
- Полученное значение делим на 5. Получаем кол-во кирпичей, которые нужно купить.
- Полученное частное умножаем по очереди на числа из 2-го столбца таблицы («Цена кирпича»). Т.о., получаем стоимости всех кирпичей от разных поставщиков.
- Для поставщика А: полученное произведение (см.п.2) суммируем с данным из 3-го столбца («Стоимость доставки»). Получаем полную стоимость покупки с учетом доставки.
- Для поставщиков Б и В учитываем «Специальные условия» из 4-го столбца таблицы.
Решение:
20 тонн = 20 000 кг.
20 000 : 5 = 4000 (шт.) кирпичей требуется купить.
Поставщик А. Стоимость кирпичей равна:
4000·49=196 000 (руб.).
Полная стоимость покупки:
196 000+8000=204 000 (руб.).
Поставщик Б. Стоимость кирпичей:
4000·55=220 000 (руб.).
Сумма заказа больше 200 000 руб. Тогда согласно «Специальным условиям», доставка производится бесплатно, и полная стоимость составляет: 220 000 (руб).
Поставщик В. Стоимость кирпичей:
4000·62=248 000 (руб.).
Эта сумма больше, чем 240 000 руб., поэтому по «Специальным условиям» на доставку предоставляется скидка 50%, и стоимость доставки равна
6000:100·50=3000 (руб.).
Отсюда полная стоимость:
248 000+3000=251 000 (руб.).
Вывод: самый дешевый вариант обойдется в 204 000 рублей.
Вариант 12МБ10
[su_note note_color=»#defae6″]
В трех салонах сотовой связи один и тот же смартфон продается в кредит на разных условиях. Условия приведены в таблице.

Определите, в каком из салонов покупка обойдется дешевле всего (с учетом переплаты). В ответ запишите стоимость этой покупки в рублях.
[/su_note]
Алгоритм выполнения
- Для вычисления полной стоимости покупки найдем величину первоначального взноса и прибавим к ней сумму, которую придется внести в виде всех ежемесячных платежей.
- По этой формуле рассчитываем стоимость смартфона для всех 3-х салонов. Находим наименьшее значение.
Решение:
Создаем формулу для расчета итоговой стоимости. Она должна выглядеть так: СтоимостьСмартфона · ПервоначальныйВзнос(%) + СрокКредита ·СуммаПлатежа.
Расчет для салона «Эпсилон»: 19800·0,1+6·3200=1980+19200=21180 (руб.).
Расчет для салона «Дельта»: 20200·0,1+12·1580=2020+18960=20980 (руб.).
Расчет для салона «Омикрон»: 20800·0,2+6·2900=4160+17400=21560 (руб.).
Наименьшим среди полученных чисел является 20980. Это значит, что дешевле всего покупка обойдется в салоне «Дельта».
Ответ: 20980.
Вариант 12МБ11
[su_note note_color=»#defae6″]
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
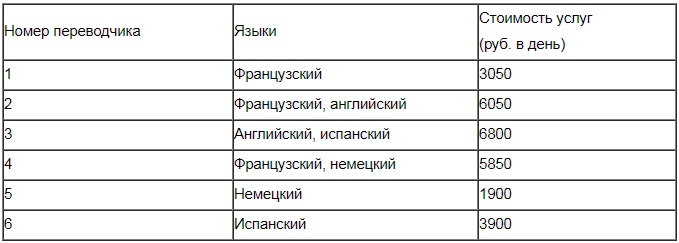
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют всеми четырьмя языками: английским, немецким, испанским и французским, а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения
- Рассматриваем переводчиков, для которых указано по 2 языка. Делаем вывод о том, что использовать 2 таких переводчика не представляется возможным, поскольку в одном случае суммарная стоимость их услуг превышает допустимый бюджет, в других – дублируются языки.
- Учитываем, что 5-й переводчик «стоит» значительно дешевле остальных, а потому его желательно нанять.
- Отказываемся от переводчика №4, поскольку в этом случае дублируется немецкий язык.
- Выбираем из переводчиков №№ 2 и 3 (владеющих двумя языками) того, который «стоит» дешевле.
- Из оставшихся переводчиков №№ 1 и 6 выбираем того, чей язык еще не привлечен.
Решение:
Мы не можем взять пару переводчиков с двумя языками, т.к.:
- у переводчиков №2 и №3, а также №2 и №4 дублируются языки. В 1-м случае это английский, во 2-м – французский;
- у переводчиков №3 и №4 суммарная стоимость услуг больше, чем 12 000 руб. Проверяем: 6800+5850=12 650 (руб.).
Точно стоит нанять в данной ситуации переводчика №5, поскольку его услуги стоят дешевле всего (1900 руб.). А тогда нужно отказаться от переводчика №4 по причине дублирования у него немецкого языка.
Вторым возьмем переводчика №2. Он владеет 2-мя языками и при этом «стоит» дешевле переводчика №3 (тоже двуязычного).
Из оставшихся переводчиков №1 и №6 отказываемся от №1, т.к. французский язык уже представлен у переводчика №2.
Итак, получаем группу из №№2,5,6. Проверяем, что суммарная стоимость их услуг укладывается в требуемые 12 000 рублей: 6050+1900+3900=11 850 (руб.)
Ответ: 256
Вариант 12МБ12
[su_note note_color=»#defae6″]
В таблице даны результаты олимпиад по физике и химии в 10 «А» классе.
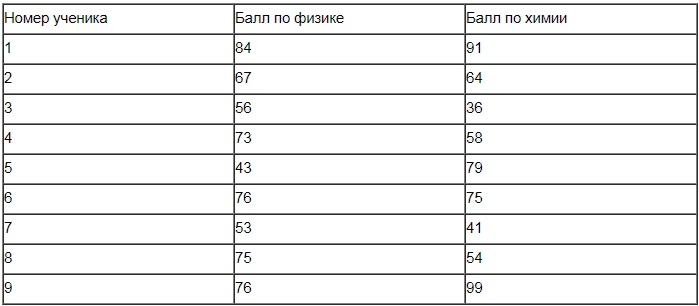
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 130 или хотя бы по одному предмету набрано не меньше 70 баллов.
Укажите номера учащихся 10 «А», набравших меньше 70 баллов по физике и получивших похвальные грамоты, без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения
- Анализируем 2-й столбец таблицы («Балл по физике»), отбрасываем все номера учеников, получивших больше 70 баллов.
- Для оставшихся проверяем, какой они получили балл по химии (в 3-м столбце таблицы). Если балл равен 70 или больше, то фиксируем номер обладателя такого результата для ответа. Если нет, то суммируем полученные баллы и проверяем, больше их сумма или нет. Номера учеников, получивших 130 баллов или больше, тоже фиксируются для ответа.
Решение:
Во 2-м столбце таблицы имеется 4 ученика, которые набрали по физике меньше 70 баллов. Их номера – 2, 3, 5 и 7.
Балл по химии у ученика №2 равен 64. Это меньше 70, однако найдя сумму 67 (по физике) и 64 (по химии), получаем 131. Отсюда делаем вывод: ученик №2 получил грамоту.
Балл по химии у ученика №3 составляет 36 баллов. 36<70, поэтому находим сумму баллов:
56+36=92.
92<130, а, следовательно, ученик №3 не получил грамоту.
У ученика №5 балл по химии – 79. Это превышает граничные 70 баллов, поэтому ученик №5 получил грамоту.
Ученик №7 заработал по химии 41 балл. Т.к. этот бал меньше 70, то нужно искать сумму баллов по обоим предметам.
Считаем:
53+41=94.
94<130, из чего делаем вывод, что ученик №7 не получил грамоту.
Ответ: 25
Вариант 12МБ13
[su_note note_color=»#defae6″]
Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 500 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды.
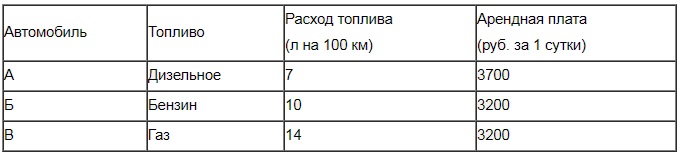
Помимо аренды, клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива – 25 рублей за литр, бензина – 35 рублей за литр, газа – 20 рублей за литр. Сколько рублей заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
[/su_note]
Алгоритм выполнения
- Разрабатываем формулу для вычисления издержек, связанных с арендой автомобиля для каждого из случаев. В ней следует цену топлива умножить на расход топлива на 100км, а затем на 5 (поскольку расход топлива приведен для каждых 100 км, а всего придется проехать 500 км). Далее к полученному произведению следует прибавить арендную плату.
- Рассчитываем по этой формуле издержки для автомобилей А, Б и В.
- Сравниваем полученные результаты, находим минимальный.
Решение:
Расчетная формула для определения издержек на автомобиль в общем виде такова:
ЦенаТоплива · РасходТоплива · 5+ АренднаяПлата.
Здесь под множителем «ЦенаТоплива» понимается стоимость 1 л топлива (данные приведены после таблицы). «РасходТоплива» – данные из 3-го столбца таблицы. «АренднаяПлата» – данные из 4-го столбца таблицы.
Считаем:
автомобиль А: 25·7·5+3700=875+3700=4575 (руб.)
автомобиль Б: 35·10·5+3200=1750+3200=4950 (руб.)
автомобиль В: 20·14·5+3200=1400+3200=4600 (руб.)
Наименьшая среди полученных сумм – 4575 рублей.
Ответ: 4575.
Вариант 12МБ14
[su_note note_color=»#defae6″]
Алексею нужен пылесос. В таблице показано 6 предложений от разных магазинов и их удаленность от дома Алексея.
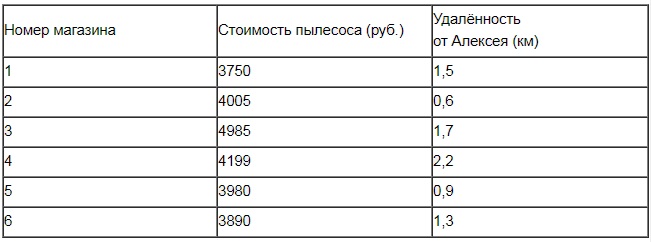
Алексей хочет купить пылесос в магазине, который находится не дальше 1,2 км от него. Найдите наименьшую стоимость пылесоса в магазинах (из представленных), удовлетворяющих данному условию. Ответ дайте в рублях.
[/su_note]
Алгоритм выполнения
- Используя имеющуюся в условии оговорку, что удаленность магазина должна быть не большей, чем 1,2 км, отбрасываем магазины с чрезмерной удаленностью.
- Из оставшихся магазинов выбираем тот, который предлагаем наименьшую цену пылесоса.
Решение:
Находим номера магазинов, которые удалены от дома Алексея на расстояние, большее чем 1,2 км. Это №№ 1, 3, 4, 6. Т.о, подходят Алексею магазины под номерами 2 и 5.
Магазин №2 предлагает пылесосы по цене 4005 руб., №5 – по цене 3980 руб. Отсюда делаем вывод: наименьшая стоимость равна 3980 рублей.
Ответ: 3980.
Вариант 12МБ15
[su_note note_color=»#defae6″]
Интернет-провайдер предлагает три тарифных плана.
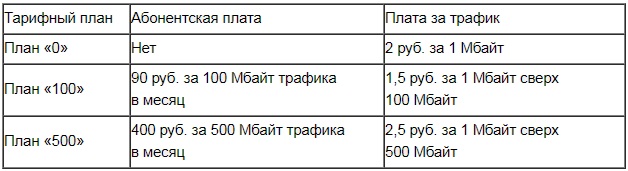
Пользователь предполагает, что его трафик составит 350 Мбайт в месяц, и исходя из этого выбирает наиболее дешевый тарифный план. Сколько рублей должен будет заплатить пользователь за месяц, если его трафик действительно будет равен 350 Мбайт?
[/su_note]
Алгоритм выполнения
- Отбрасываем план «500», поскольку его трафик не равен 350 Мбайт.
- Просчитываем стоимость платы за трафик для плана «0». Для этого множим 350 Мбайт на 2 руб.
- Просчитываем стоимость оплаты за план «100». Для этого к 90 руб. (за первые 100 Мбайт) прибавляем стоимость остальных необходимых 250 Мбайт. Для вычисления стоимости 250 Мбайт делаем следующее: 250 умножаем на 1,5 (см. условие, прописанное в 3-м столбце таблицы для плана «100»).
- Сравниваем полученные в пп.1 и 2 результаты между собой. Находим наименьшее значение.
Решение:
План «500» по условию задачи изначально не подходит. Поэтому его при поиске самого дешевого варианта не учитываем.
Для плана «0» имеем: 350·2=700 (руб.) – будет стоить ежемесячная плата для пользователя.
Для плана «100» получим: 90+250·1,5=590 (руб.) – за месяц в целом с учетом абонплаты.
Сравниваем стоимость планов «0» и «100» между собой. Делаем вывод: стоимость плана «100» меньше.
Ответ: 590.
Вариант 12МБ16
[su_note note_color=»#defae6″]
На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 трем спортсменам. Результаты приведены в таблице.
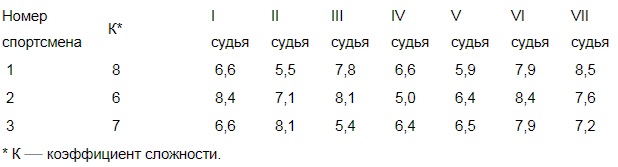
Итоговый балл вычисляется следующим образом: две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются, и их сумма умножается на коэффициент сложности.
В ответе укажите номера спортсменов, итоговый балл которых больше 140, без пробелов, запятых и других дополнительных символов.
[/su_note]
Алгоритм выполнения
- Подсчитываем итоговый балл для каждого спортсмена на основании формулы, прописанной в условии задания.
- Сравниваем полученные результаты с граничным значением 140.
Решение:
Для 1-го спортсмена. 2 наибольшие оценки: 8,5 и 7,9. 2 наименьшие оценки: 5,5 и 5,9. Оставшиеся: 6,6; 7,8; 6,6. Итоговый балл: (6,6+7,8+6,6)·8=168.
Для 2-го спортсмена. 2 наибольшие оценки: 8,4 и 8,4. 2 наименьше оценки: 5,0 и 6,4. Оставшиеся: 7,1; 8,1; 7,6. Итоговый балл: (7,1+8,1+7,6)·6=136,8.
Для 3-го спортсмена. 2 наибольшие оценки: 8,1 и 7,9. 2 наименьшие оценки: 5,4 и 6,4. Оставшиеся: 6,6; 6,5; 7,2. Итоговый балл: (6,6+6,5+7,2)·7=142,1.
Сравниваем:
168>140; 136,8<140; 142,1>140.
Ответ: 13.
Вариант 12МБ17
[su_note note_color=»#defae6″]
Для транспортировки 42 тонн груза на 1200 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей каждого перевозчика указаны в таблице.

Сколько рублей придется заплатить за самую дешевую перевозку?
[/su_note]
Алгоритм выполнения
- Сначала определяем стоимость 1 грузоперевозки от перевозчика А. Для этого 1200 делим на 100 и умножаем на число из 2-го столбца таблицы для перевозчика А. Затем находим количество автомобилей, необходимых для перевозки 42 т груза. Для этого 42 делим на число из 3-го столбца для перевозчика А. Далее перемножаем 2 полученных числа.
- Выполняем аналогичные расчеты для перевозчиков Б и В.
- Находим среди полученных результатов минимальный.
Решение:
Для перевозчика А. Стоимость 1 грузоперевозки составляет:
1200:100·3100=37 200 (руб.).
Автомобилей при этом потребуется
42:4=10,5, т.е. 10+1=11.
Полная стоимость перевозки равна:
37 200·11=409 200 (руб.).
Для перевозчика Б. Стоимость 1 грузоперевозки:
1200:100·4000=48 000 (руб.).
Автомобилей для этого потребуется:
42:5,5≈7,64, т.е. 7+1=8.
Полная стоимость:
48 000·8=384 000 (руб.).
Для перевозчика В. Цена 1 грузоперевозки:
1200:100·7600=91 200 (руб.).
Автомобилей для этого нужно:
42:10=4,2, то есть 4+1=5.
Полная стоимость:
91 200·5=456 000 (руб.).
Сравнивая полученные результаты, видим, что наименьшую полную стоимость предлагает перевозчик Б.
Ответ: 384000.