Задачи на финансы
17 задание профильного уровня ЕГЭ по математике представляет собой задачу, связанную с финансами, а именно эта задача может быть на проценты, часть долгов и др. Сложность заключается в том, что необходимо рассчитать проценты или часть на длительном промежутке, поэтому данная задача не является прямой аналогией стандартных задач на проценты. Чтобы не говорить об общем, перейдем непосредственно к разбору типовой задачи.
Разбор типовых вариантов заданий №17 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=»#defae6″]
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей.
Условия его возврата таковы:
- 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0.6 | 0.4 | 0.3 | 0.2 | 0.1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
[/su_note]
Алгоритм решения:
- Рассматриваем, какова величина выплат по кредиту ежемесячно.
- Определяем долг по каждому месяцу.
- Находим величину требующихся процентов.
- Определяем сумму выплат за весь период.
- Вычисляем процент r суммы выплат долга.
- Записываем ответ.
Решение:
1. По условию, долг банку ежемесячно должен уменьшаться в таком порядке:
1; 0,6; 0,4; 0,3; 0,2; 0,1; 0.
2. Пусть k = 1 + r / 100, тогда долг каждый месяц равняется:
k; 0,6k; 0,4k; 0,3k; 0,2k; 0,1k.
3. Значит, выплаты со 2-го по 14-е ежемесячно составляют:
k — 0.6; 0.6k — 0.4; 0.4k — 0.3; 0.3k — 0.2; 0.2k — 0.1; 0.1k
4. Вся сумма выплат равна:
![]()
По условию, весь размер выплат меньше 1,2 млн руб, следовательно,
![]()
Наибольшим целым решением получившегося неравенства является 7. Тогда оно и есть искомое – 7.
Ответ: 7%.
Второй вариант (из Ященко, №1)
[su_note note_color=»#defae6″]
В июле 2020 года планируется взять кредит в банке на сумму 300 000 рублей. Условия его возврата таковы:
- каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите r, если известно, что кредит будет полностью погашен за два года, причём в первый год будет выплачено 160 000 рублей, а во второй год — 240 000 рублей.
[/su_note]
Алгоритм решения задачи:
- Определяем величину денежного долга.
- Вычисляем сумму задолженности после первого взноса.
- Находим величину долга после второго взноса
- Находим искомый процент.
- Записываем ответ.
Решение:
1. В долг было взято 300 000 рублей. По условию сумма долга, подлежащего возврату увеличивается на r%, а значит в ![]() раз. Для выплаты долга необходимо отдать банку 300000∙k.
раз. Для выплаты долга необходимо отдать банку 300000∙k.
2. После внесения платежа, равного 160 000 рублей. Остаток долга равняется
![]() руб.
руб.
3. На следующий год остаток тоже возрастет в k раз и составит:
![]()
Вносимая сумма равна 240 000 рублей:
![]() рублей.
рублей.
4. Поскольку согласно условию эти выплаты погасят весь долг, получаем квадратное уравнение:
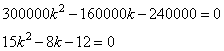
Решаем его, с помощью формул дискриминанта и корней:
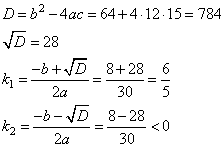
5 .Среди полученных корней один отрицательный и условию не удовлетворяет. Получаем:
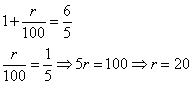
Таким образом, брать кредит планируется под 20% .
Ответ: 20%.