Задание №4 ОГЭ по физике

Движение по окружности. Простые механизмы. Колебания и волны. Движение тела под действием силы тяжести.

Для успешного решения задания №4 необходимо знание тем и разделов, приведенных в заглавии. Т.е. это материалы частично из раздела динамики (криволинейное движение, силы в природе), частично из раздела статики. Кроме того, для решения может потребоваться понимание колебательных процессов. Полезные сведения даны в разделе теории.

Теория к заданию №4 ОГЭ по физике

Равномерное движение по окружности

Движение тела по окружности можно свести к движению по очень коротким прямым линиям (хордам), которые складываются в замкнутую криволинейную траекторию. Такой подход позволяет рассматривать движение в каждый момент времени как прямолинейное и говорить о перемещении, скорости и ускорении такого движения в привычном их понимании.

В каждой точке окружности тело имеет мгновенную скорость, вектор которой совпадает с вектором перемещения в этой точке и, следовательно, направлен по касательной к окружности. При этом модуль скорости не изменяется, что и делает движение равномерным.

Ускорение в каждой точке окружности направлено к ее центру. Т.е. при движении по окружности с постоянной скоростью тело испытывает ускорение. В этом особенность такого движения, которая и обеспечивает соответствующую траекторию. Связана она с тем, что векторы скорости и ускорения имеют между собой прямой угол, и их результирующая (определяемая по правилу треугольника) удерживает тело от движения по касательной, заставляя его смещаться и держаться на одинаковом расстоянии от центра окружности.

Центростремительное ускорение может быть вычислено по формуле:

,

где R – радиус окружности.

Блоки

Блок в физике – это простой механизм, обеспечивающий возможность регулирования силы, действующей на связанные с ним тела. Блок представляет собой колесо некоторой толщины с выемкой (желобом) по своей окружности. Обязательное условие для блока – возможность вращаться вокруг своей оси. По желобу проходит ремень (цепь, канат, веревка и т.д.), контакт с которым и обеспечивает вращение блока.

Блок может быть неподвижным и подвижным. Первый имеет неподвижную (зафиксированную) ось вращения, второй – подвижную.

Всякий блок – это рычаг, причем неподвижный является равноплечим рычагом, а подвижный имеет плечи, длины которых относятся между собой как 1:2. Из того, что блоки это рычаги, следует, что для них справедливо правило: проигрыш в расстоянии обеспечивает равную величину выигрыша в усилии (т.е. в силе).

Условие равновесия тела (правило моментов)

Если тело имеет неподвижную ось вращения, то оно находится в равновесии при условии, что сумма (алгебраическая) всех моментов сил, приложенных к телу, равна нулю относительно данной неподвижной оси.

Математическое выражение условия равновесия:

 .

Момент силы при этом можно вычислить по формуле:

 ,

где F – приложенная сила, l – плечо силы (кратчайшее расстояния от прямой, на которой находится  до оси вращения).

Движение тела по вертикали

Речь в данном случае идет о движении тел, брошенных вертикально вверх или опускающихся вертикально вниз. И в первом, и во втором случае имеется в виду, что на тела действует только сила тяжести, а сопротивление воздуха отсутствует.

Если тела движутся исключительно под действием силы тяжести, то это движение является равноускоренным, причем ускорение всегда одинаково. Это – ускорение своб.падения g. Величина ускорения для Земли:  . Если тело движется вверх, то  , если падает вниз, то  .

При таком движении тела скорость и высота могут быть найдены по формулам:

,

 .

Знак «–» в формулах перед g соответствует ситуации, когда тело движется вверх, поскольку в этом случае направления векторов скорости и ускорения противоположны.

Движение тела вниз под действием силы тяжести без начальной скорости (т.е. в ситуации, когда его просто отпускают, а не бросают), называют свободным падением.

Период колебания маятника

В механике различают маятники математические и пружинные. Разница между ними заключается в том, что в первом случае тело скреплено с пружиной, а во втором – подвешено на тонкой неупругой нити. Соответственно, в пружинном маятнике тело колеблется по прямой линии, то удаляясь от положения равновесия, то возвращаясь в него, а в математическом – колеблется по дуге влево и вправо от положения равновесия.

Период колебания в пружинном маятнике вычисляется так:

.

где m – масса тела, k – жесткость пружины.

Период колебаний математического маятника:

,

где l – длина нити, на которой подвешено тело.

Волны

В самом общем случае под волной понимают распространение колебаний от частицы к частице и от точки к точке. Различают волны механические, звуковые и др. Параметрами, описывающими характер распространения волны, являются ее длина (λ), частота (  ), период (Т), амплитуда (А). Кроме того, говорят о скорости распространения (v) волн. Эти величины связаны между собой различными соотношениями, например:

Разбор типовых вариантов заданий №4 ОГЭ по физике

Демонстрационный вариант 2018

[su_note note_color=»#defae6″]

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью υ0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Полная механическая энергия тела на некоторой промежуточной высоте h равна

[/su_note]

Алгоритм решения:
  1. Записываем уравнение з-на сохранения энергии. Используя его, анализируем его и определяем полную энергию в граничных точках – в момент броска и при достижении телом максимальной высоты.
  2. Определяем полную энергию для тела в произвольный промежуточный момент времени, т.е. после того, как тело уже подброшено, но еще не достигло максимальной высоты.
  3. Записываем ответ.
Решение:
  1. Поскольку в условии есть оговорка о том, что сопротивлением воздуха можно пренебречь, то можно использовать з-н сохранения энергии. Полная энергия тела в любой момент времени, согласно закону, равна: 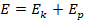 . Т.к. изначально тело бросают с поверхности земли с ненулевой скоростью (по условию – со скоростью v0), то в нач.момент времени  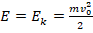, т.е. имеет максимальную кинетич.энергию и равную нулю потенциальную. Когда тело достигает максимальной высоты, это значит, что его движение остановилось (  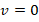) и тело находится в покое на некоторой высоте над землей. В этот момент тело имеет максимальную потенц.энергию при нулевой кинетической: .
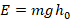  2. В процессе подъема тело одновременно находится в движении (его скорость уже не равна v0, а имеет меньшее значение v) и в то же время является телом, поднятым над землей на некую высоту h. Это значит, что полная энергия на промежуточной высоте должна быть выражена уравнением: 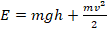. Такого варианта ответа среди предложенных нет. Однако среди них есть вариант 2: 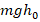. Он содержит выражение для полной энергии в момент максимального подъема тела. Поскольку по з-ну сохранения энергии ее значение одинаково в любой момент времени, то это значит, что вариант 2 хотя и не содержит подробной расчетной формулы для вычисления полной энергии на высоте h, но отражает ее правильное количественное значение. А следовательно, именно вариант 2 является единственно правильным в данном случае.

Ответ: 2

Первый вариант (Камзеева, № 3)

[su_note note_color=»#defae6″]

Легкий рычаг находится в равновесии под действием двух сил (см. рис.)

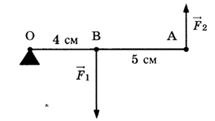
Отношение модуля силы F1 к модулю силы F2 равно

  1. 1,25
  2. 2,25
  3. 1,8
  4. 0,8

[/su_note]

Алгоритм решения:
  1. Переведем в СИ величины ОВ и ВА.
  2. Записываем ур-ние равновесия рычага.
  3. Записываем формулу для вычисления момента. Преобразуем ее для М1 и М2.
  4. Находим искомое отношение сил, используя ур-ние равновесия рычага (1).
  5. Записываем ответ.
Решение:
  1. Переведем в СИ данные в условии расстояния: ОВ=4 см=0,04 м; ВА=5 см=0,05 м.
  2. Согласно условию равновесия, имеем: 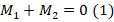. Здесь М1 и М2 – соответственно моменты для F1 и F2. Примем, что положительным будет момент, направленный по часовой стрелке. Тогда получаем, что  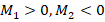(можно и наоборот).
  3. Момент силы определяется по формуле: 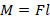 . Т.к. 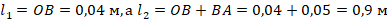, то .
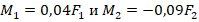  4. Подставим выражения для моментов в (1). Получим: 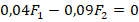. Отсюда: .

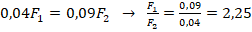Ответ: 2

Второй вариант (Камзеева, № 7)

[su_note note_color=»#defae6″]

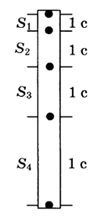
Для тела, свободно падающего из состояния покоя у поверхности некоторой планеты, измерялись расстояния, проходимые телом за последовательные равные промежутки времени (см. рис.). Чему равно ускорение свободного падения на планете, если S2=30 м? Сопротивление атмосферы пренебрежимо мало.

  1. 5 м/с2
  2. 10 м/с2
  3. 20 м/с2
  4. 40 м/с2

[/su_note]

Алгоритм решения:
  1. Выражаем S1 через S2. Находим S1.
  2. Записываем формулу для S1 через ускорение. Выражаем из нее искомое ускорение. Вычисляем ускорение.
  3. Записываем ответ.
Решение:
  1. Известно, что при равноускоренном движении пути, проходимые телом за одинаковые временные промежутки относятся как ряд нечетных натуральных чисел, а именно: 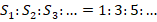. Исходя из этого: .
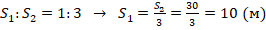  2. Поскольку тела начинает двигаться из состояния покоя ( 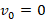 ), то 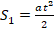 . Отсюда:  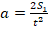. Т.к. S1 – это путь за первую секунду, то t=1c. Тогда получаем: .

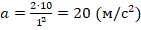Ответ: 3

Третий вариант (Камзеева, № 11)

[su_note note_color=»#defae6″]

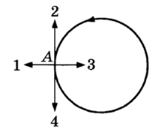
Тело движется равномерно по окружности против часовой стрелки (см. рис.). Какое направление имеет вектор ускорения в точке А?

  1. 1
  2. 2
  3. 3
  4. 4

[/su_note]

Алгоритм решения:
  1. Анализируем условие. Определяем вид ускорения. Находим правильный вариант ответа.
  2. Записываем ответ.
Решение:

Поскольку имеет место равномерное движение тела по окружности, то оно испытывает единственное ускорение – центростремительное. Его вектор всегда направлен к центру окружности. Следовательно, в т.А правильное направление – под номером 3.

Ответ: 3

Текст: Базанов Даниил, 5.9k 👀