Задание 15МО2 (схема метро)
На рисунке изображена схема метро в городе N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Веселая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная. Всего в метрополитене города N есть три станции, от которых тоннель ведет только в одну сторону – это станции Дальняя, Верхняя и Звездная. Максим живет недалеко от станции Надежда.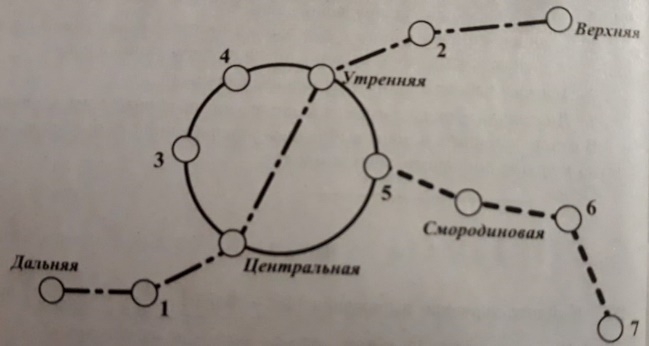
📜Теория для решения:
Посмотреть решение
Задание №1
Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры |
Решение: для того, чтобы правильно определить номера станций, необходимо при чтении информации выделять (подчеркивать) их как в тексте, так и сразу же подписывать на рисунке. Ниже показана часть текста, в которой подчеркнуты основные моменты, а также расстановка станций, которая выполняется сразу по ходу чтения текста.
Станция Ветреная расположена между станциями Центральная и Дальняя (значит, это номер 1). Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя (сразу видно, что двигаться надо от Центральной к Утренней, значит, Быстрая будет под номером 5), Птичья и Веселая (соответственно 4 и 3, так как двигаемся по кольцу). Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная (видим эту ветку справа нижнюю, соответственно Хоккейная – номер 6, а Звездная – 7). Максим живет недалеко от станции Надежда (она под номером 2, так как осталась одна не указанная).
Теперь расставляем номера необходимых объектов в таблицу:
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры | 6 | 2 | 4 | 1 |
В бланк записываем ответ: 6241
Задание №2
Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяженностью 8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 500 метров. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Решение: для того, чтобы узнать, сколько дней был закрыт проезд, нужно узнать, сколько рабочих дней они прокладывали рельсы. По условию длина участка 8 км, переводим ее в метры, так как в 1 день меняли по 500 метров. Получаем 8000 метров. Теперь делим 8000 метров на 500 метров, получаем 16 рабочих дней трудилась бригада. Нам надо узнать, сколько дней всего был закрыт проезд, так как в выходные работ не было, а проезд был закрыт. По условию работы начались с понедельника, значит бригада работала 3 полных недели и 1 понедельник на четвертой неделе (16 дней делим на 5 рабочих в неделю, получается 3 недели и 1 остается – понедельник). После каждой недели у нас два дня выходных: 2 после первой, 2 после второй, 2 после третьей. Таким образом, 6 выходных был закрыт проезд. Значит, 16 рабочих и 6 выходных, это 22 полных дня был закрыт проезд.
Записываем ответ 22 в бланк.
Задание №3
Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в квадратных километрах), если длина кольцевой ветки равна 32 км. В ответе укажите S*.
Решение: так как известна длина кольцевой ветки, то это значит, что мы имеем длину окружности (по условию – кольцевая ветка – это окружность). Длина окружности вычисляется по формуле 2πR. Значит, 2πR=32. Делим обе части на 2, получаем πR=16. Находим радиус, для этого надо 16 разделить на число π. То есть R=16/π. Формула площади круга S=πR2. Подставляем в нее вместо радиуса 16/π. Получаем, что S=π(16/π) 2. Возводим в квадрат, получаем S=π(256/π2). Теперь сокращаем числитель и знаменательна число π. Получается, что S=256/π . Поскольку в задании есть указание, что в ответ надо записать S* , то умножая эти величины в нашей формуле S=256/π, получаем, что S*= 256. Записываем ответ 256 в бланк.
Задание №4
Найдите расстояние (по железной дороге) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 14 км, расстояние от Звездной до Смородиновой 11 км, а от Быстрой до Хоккейной – 7 км. Все расстояния даны по железной дороге.
Решение: итак, Радужная ветка – это станции Быстрая, Смородиновая, Хоккейная и Звездная. Можно для удобства сделать чертеж и обозначить на нем станции первыми буквами их названий и расставить длины. Получится вот такой рисунок, по которому можно легко определить расстояние от Смородиновой (С) до Хоккейной (Х).
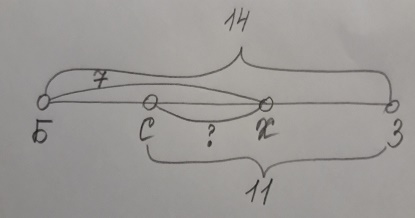
Для этого из длины отрезка СЗ=11 нужно вычесть длину отрезка БХ=7, получим длину СХ=4. В бланк записываем число 4.
Задание №5
Школьник Максим в среднем за месяц совершает 45 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Максим уедет из города к бабушке в деревню и неиспользованные карточки обнулятся. Во сколько рублей обойдется самый дешевый вариант?
| Количество поездок | Стоимость одной поездки
(в рублях) |
Дополнительные условия |
| 1 | 40 | Школьникам скидка 20% |
| 10 | 37 | Школьникам скидка 10% |
| 30 | 35 | Школьникам скидка 10% |
| 50 | 32 | Нет |
| Безлимит | — | Любое число поездок в течение месяца за 2000 рублей |
Решение: для решения этого задания необходимы данные только из таблицы. Итак, нужно совершить 45 поездок за наименьшую стоимость. Значит, два последних варианта не подходят, так как 50 поездок – это много, деньги на карте обнулятся, а по Безлимиту в среднем приблизительно выйдет одна поездка 44 рубля (2000 : 45 поездок), скидки здесь не предусмотрены. Следовательно, будем составлять наборы из первых трех вариантов, а затем выбирать самый дешевый.
Для удобства надо посчитать каждый из трех вариантов, как карточку для школьника, т.е. с указанной скидкой. Затем посчитать стоимость каждой карточки полностью. Вспомним, чтобы найти количество процентов от данного числа, надо число разделить на 100 и умножить на количество процентов. Запишем это решение в таблице.
| Количество поездок | Стоимость одной поездки
(в рублях) |
Стоимость одной поездки для школьника
(в рублях) |
Стоимость 1 карточки для школьника
(в рублях) |
| 1 | 40 | 40-40:100*20=32 | 1*32=32 |
| 10 | 37 | 37-37:100*10=33,3 | 10*33,3=333 |
| 30 | 35 | 35-35:100*10=31,5 | 30*35=945 |
- Допустим, что можно купить из первого варианта 45 карточек по 32 руб. Тогда получим, что 32*45=1440 руб.
- Допустим, что можно купить на 45 поездок: одну третью (на 30 поездок), 1 вторую (на 10 поездок) и пять первых (на пять поездок). Рассчитаем стоимость.
Одна третья карточка на 30 поездок – это 945 рублей.
Одна вторая карточка на 10 поездок – это 333 рубля.
Пять первых карточек: 32*5=160 рублей.
Теперь складываем стоимость всех карточек. 945+333+160=1438 рублей. Это уже меньше, чем в решении 1.
- Допустим, что можно купить 1 третью карточку (на 30 поездок) и 15 первых, так как это тоже 45 поездок. Одна третья карточка на 30 поездок – это 945 рублей. 15 первых будут стоить 15*32=480 рублей. Складываем стоимости 945 и 480, получаем 1425 рублей.
- Допустим, что можно еще купить 4 вторых (на 40 поездок) и 5 первых карточек. Тогда 4*333=1332 руб; 5*32=160 руб. Вместе это составит 1332+160=1492 рубля.
Записываем в ответ число 1425, так как это самый дешевый вариант из всех.
Ответ: см. в решении