Задание 15MO05 (шины) • СПАДИЛО

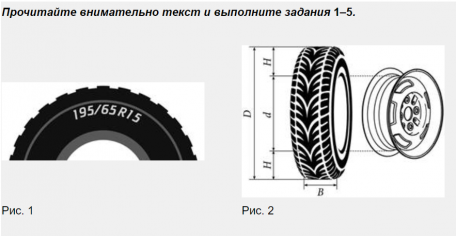
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис.1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (65 в приведенном примере) – процентное отношение высоты боковины (параметр Н на рисунке 2) к ширине шины, то есть 100• $\frac{Н}{В}$ . Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.

За обозначением типа конструкции шины идет число, указывающее диаметр d диска колеса в дюймах ( в 1 дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.

Завод производит внедорожники определенной модели и устанавливает на них колеса с шинами маркировки 215/65 R16.

📜Теория для решения:

Посмотреть решение

Задание №1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешенные размеры шин.

Ширина шины (мм)	Диаметр диска (дюймы)
Ширина шины (мм)	16	17	18
215	215/65	215/60	—
225	225/65; 225/60	225/55	—
235	235/60	235/55; 235/50	235/50

Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.

Решение

Смотрим по таблице на столбец, где указан диаметр диска – 17 дюймов. Движемся по столбцу вниз и просматриваем первые числа (ширину шины) в маркировках, нам надо найти наибольшую, в последней строке – это число 235. Значит наш ответ 235.

Ответ: 235

Задание №2. На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки 275/50 R17?

Решение

Прежде всего мы должны понимать, что высота колеса (диаметр колеса D) состоит из высоты шины Н, а их две, а также из диаметра диска . Если изобразить это в виде геометрического рисунка, то он будет выглядеть так, как показано на рисунке 2:

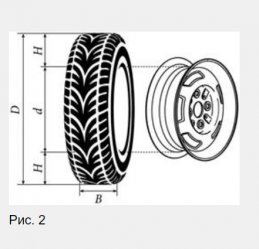
Значит, D=2H + d. Для удобства и последовательного решения задачи лучше составить таблицу, в которой и будем всё решать. В верхней строке записаны данные из условия. В первом столбце выписаны все параметры, которые будем находить.

Таблица 1

	1 колесо 215/55 R17	2 колесо 275/50 R17
Высота Н
Диаметр диска d
Диаметр колеса D
Радиус колеса
Разница в радиусах

Теперь начинаем заполнять каждую строчку для 1 и 2 колеса, проводя вычисления.

	1 колесо 215/55 R17	2 колесо 275/50 R17
Высота Н	Запоминаем: для нахождения высоты выражаем второе число десятичной дробью и умножаем на первое число (так как второе число – процентное отношение высоты боковины к ширине шины). Чтобы выразить число % десятичной дробью, надо разделить его на 100!
	55/100 $∙$ 215=0,55 $∙$ 215=118,25	50/100 $∙$ 275=0,5 $∙$ 275=137,5
Диаметр диска d	Так как диаметр диска дан в дюймах, то надо умножить последнее число маркировки шины (17) на количество дюймов в 1 мм, т.е. на 25,4
	17 $∙$ 25,4=431,8	431,8
Диаметр колеса D	В начале решения нашей задачи, мы выяснили как найти диаметр колеса, это надо запомнить! D=2H + d. Находим диаметр в каждом случае, используя данные, которые нашли выше.
	2 $∙$ 118,25 + 431,8=668,3	2 $∙$ 137,5 + 431,8=706,8
Радиус колеса	Помним, что радиус, это половина диаметра
	668,3:2=334,15	706,8:2=353,4
Разница между радиусами	Для того, чтобы ответить на вопрос задания, надо найти разность между найденными радиусами
	353,4 – 334,15=19,25

Ответ: 19,25

Задание №3. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 235/50 R18?

Решение

Решение данного задания будем строить по принципу задания 2, так как требуется найти разницу в диаметрах между шинами заводской маркировки (смотрим в условии) 215/65 R16 и шинами маркировки 235/50 R18.

Сделаем таблицу, аналогичную таблице 1 (до строки диаметр колеса) и заполним её. Объяснения смотрим по заданию 2.

	1 колесо 215/65 R16	2 колесо 235/50 R18
Высота Н	0,65 $∙$ 215=139,75	0,5 $∙$ 235=117,5
Диаметр диска d	16 $∙$ 25,4=406,4	18 $∙$ 25,4=457,2
Диаметр колеса D	2 $∙$ 139,75 + 406,4=685,9	2 $∙$ 117,5 + 457,2=692,2
Разница между диаметрами колеса	Для того, чтобы ответить на вопрос задания, надо найти разность между найденными диаметрами
Разница между диаметрами колеса	692,2 – 685,9=6,3

Ответ: 6,3

Задание №4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Решение

С данными про колесо автомобиля, выходящего с завода (215/65 R16) мы встретились в задании 3. Надо найти диаметр, он найден в этом же задании 3 (смотрим таблицу с решением этого задания и находим соответствующее значение диаметра). Это значение равно 685,9.

Ответ: 685,9

Задание №5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 225/65 R16? Результат округлите до десятых.

Решение

Пробег автомобиля при одном обороте колеса – это длина окружности колеса. Значит, необходимо найти длину окружности, зная формулу l=2πR (данная формула есть в справочном материале ОГЭ). Зная, что диаметр – это два радиуса, формулу можем записать короче l=πD. Значение числа π не обязательно подставлять в формулу при решении задачи, удобнее использовать буквенное выражение.

Итак, нам надо найти диаметры двух колес, затем найти длины окружностей этих колес и сравнить их в процентном отношении. С маркировкой заводского колеса мы встречались, а данные ко второму колесу нужно найти. Итак, составим таблицу, аналогичную таблице 1, впишем в нее уже найденные значения заводского колеса (из задания 3) и найдем недостающие про «новое» колесо.

	1 колесо (заводское) 215/65 R16	2 колесо 225/65 R16
Высота Н	139,75	0,65 $∙$ 225=146,25
Диаметр диска d	406,4	406,4 (одинаковый с заводским)
Диаметр колеса D	685,9	2 $∙$ 146,25+406,4=698,9
Длина окружности l=πD	685,9π	698,9π

Итак, имеем две длины окружности, теперь надо найти, на сколько процентов увеличится пробег автомобиля при одном обороте колеса.

Заводское колесо 685,9π – 100%

Колесо на замену 698,9π – х %

Найдем значение х, используя правило пропорции: $\frac{698, 9 π ∙ 100}{685, 9 π} = 101, 895 \dots$ При решении числа π сократились, а значение % будет приближенное. Теперь найдем разницу между длинами окружностей 100% — 101, 895%=1,895%, округлим его, как сказано в условии – до десятых, получим 1,9 %. Наш ответ 1,9%.

Ответ: 1,9%

Общие советы и рекомендации по данному виду задач

Главное, с чем мы работаем в условии данной задачи, это маркировка шины.

Помните о том, что высота колеса – это его диаметр, состоящий из двух высот и одного диаметра диска (внутренняя металлическая часть колеса). Формулой D=2H+d придется пользоваться на протяжении нескольких заданий.

Для нахождения высоты переводим второе число маркировки в десятичную дробь (разделив на 100) и умножить его на первое число.

Используйте для решения таблицу, чтобы не запутаться при нахождении каких-либо данных.

Желаем удачи!

Ответ: см. решение

Текст: Алла Василевская, 16.7k 👀