Задание 15MO08 (зонт)

Задание №1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рисунок 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение

Так как длина зонта складывается из длины ручки и трети длины спиц, то можно найти треть длины спиц: 25 – 6,2=18,8 (см).

Так как это треть, то всю длины спицы можно найти, умножив данное число на 3: 18,8×3=56,4 (см) — длина спицы.

Ответ: 56,4

Задание №2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение

Для нахождения площади поверхности зонта надо знать площадь каждого треугольника (клина), так как из них состоит поверхность зонта.

На рисунке в условии задачи мы видим равнобедренный треугольник, у которого длина стороны а=38 см. Для нахождения площади треугольника нам нужны сторона и высота, проведенная к ней. Высота (выделена красным) по условию равна 53,1 см.

Теперь воспользуемся формулой площади треугольника (она есть в справочном материале) $S=\frac{ah}{2}=\frac{38\times 53,1}{2}=1008,9$.

Знаем, что всего таких треугольников 8, найдем площадь всей поверхности: 1008,9$\times$8=8071,2 см². Так как ответ нужно дать с округлением до десятков, то получим, что 8071,2$\approx$8070.

Ответ: 8070

Задание №3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение

Обратимся к рисунку №2, чтобы увидеть, чем конкретно является радиус сферы купола на нём.

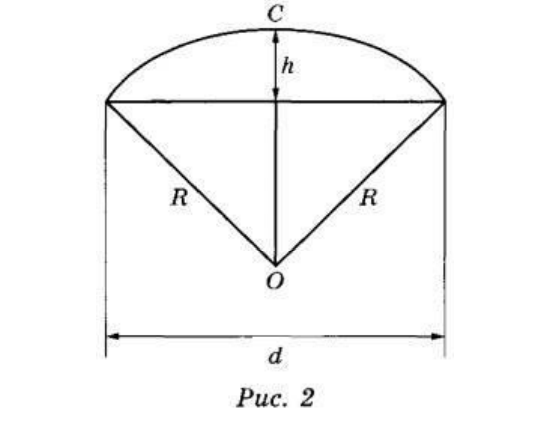
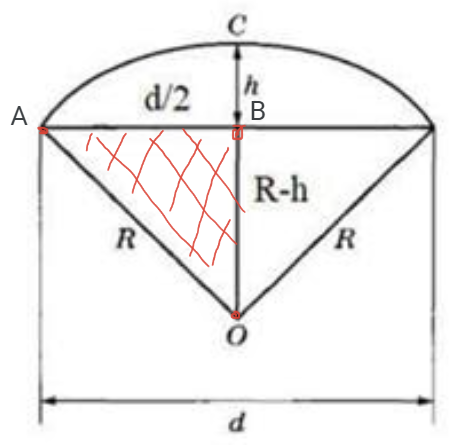
Сделаем на рисунке дополнительные обозначения: точки А и В. Получим прямоугольный треугольник АОВ, у которого гипотенуза АО=R по условию, катет АВ=d/2, тогда катет ОВ=ОС – СВ, то есть ОВ=R-h.

Теперь по теореме Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) составим равенство: АО²=АВ²+ОВ²; подставим наши данные:

R²=($\frac{d}{2})$²+ (R-h)²

Упростим наше выражение, подставим в него значения из условия задачи (h=25, d=100):

R²=$\frac{d^2}{4}$+ R²-2Rh + h² (возвели в квадрат; использовали формулу сокращенного умножения (а – в)²=а²-2ав+в²)

R²=$\frac{{100}^2}{4}$+ R²-2R$\times$ 25+ 25² (подставили числовые значения)

R²=2500+ R²-50R+ 625 (взаимоуничтожили R² и перенесли 50R в левую часть)

50R=3125

R=3125:50=62,5

Ответ: 62,5

Задание №4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение

Для решения данной задачи у нас есть всё в её условии – формула S = 2πRh и данные для того, чтобы подставить в эту формулу. Так, радиус мы нашли в задании 3 (62,5); высота известна по условию, она равна 25, число π берем как 3,14.

S = 2$\times$3,14$\times$62,5$\times$25=9812,5

Так как надо ответ округлить до целого, то 9812,5$\approx$9813

Ответ: 9813

Задание №5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение

Рассмотрим, в чем же смысл данного задания. У нас есть рулон ткани, из которой шьют зонты, отрезая необходимое количество. И, конечно же, от рулона ткани останутся обрезки. Требуется найти, сколько процентов ткани такого рулона пошло на эти обрезки.

Начнем с рулона: известна длина и ширина, следовательно, можно найти площадь всего этого рулона, т.е. 3500$\times$80=280000 см². Обратите внимание, что мы взяли 35 м=3500 см.

Теперь будем «шить» зонты, у нас их 29 штук по условию задания. Каждый зонт состоит из 8 клиньев-треугольников, то есть всего таких клиньев нам понадобится 8$\times$29=232 штуки. Зная, по условию задания, что на 1 клин-треугольник требуется 1050 кв.см ткани, найдем, сколько её понадобится на наши 232 клина: 232$\times$1050=243600 см².

Теперь из общей площади нашего рулона ткани вычтем площадь ткани для зонтов:

280000 – 243600=36400 см², это столько ткани-обрезков. Осталось ответить на вопрос задания – сколько процентов ткани рулона пошло в обрезки? Для этого данное число разделим на общую площадь ткани в рулоне и не забудем умножить на 100, так как находим ответ в процентах: 36400:280000$\times$100=13%

Ответ: 13%