Задание 15МО3 (земледельческие террасы)
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы. Земледельческие террасы – это горизонтальные площадки, напоминающие ступени. Во время дождя стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье – для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует большого ручного труда.

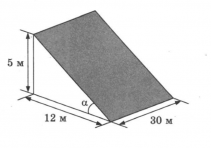
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 30 м, а верхняя точка находится на высоте 5 м от подножия.
📜Теория для решения:
Посмотреть решение
Задание №1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
Решение
Мускатный орех земледелец выращивает на склоне холма. Если смотреть на геометрический рисунок, где 5 метров – это высота холма, 30 метров – ширина участка, а 12 метров – это расстояние от подножия холма до нижней точки уклона. Таким образом, расчищенным склоном холма является прямоугольник, закрашенный на рисунке серым цветом.
Требуется найти площадь этого прямоугольника. Смотрим, что его ширина 30 м, а длина неизвестна, но она является гипотенузой прямоугольного треугольника с катетами 5 и 12 метров.
Гипотенузу найдем по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов). Обозначим гипотенузу буквой с и запишем ее нахождение: с2=122+52=144+25=169; так как √169=13, то с=13.
Теперь находим площадь расчищенного склона холма. Для нахождения S прямоугольника надо длину умножить на ширину. То есть имеем, что 13 м – это длина участка, а 30 м – ширина участка, значит S=13∙30=390 м2
В ответ запишем число 390 (наименования в бланк не пишем).
Ответ: 390
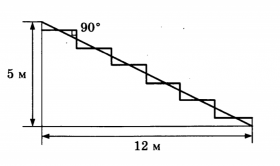
Задание №2. Земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона а, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
Решение
Во-первых, найдем тангенс по рисунку, который нам дан. Вспомним, что тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Поэтому, в нашем случае это отношение 5 к 12, то есть tq a=512. Умножим это число на 100%, как сказано в условии задачи, и посчитаем: 512×100=41, 666… Нам сказано, что необходимо округлить число до десятых, то есть оставить после запятой одну цифру (десятые доли), применив правило округления. Получим: 41, 666..≈41,7. Мы видим, что угол склона холма не превышает 50%, то есть он удовлетворяет требованиям для строительства террас. Значит, наш ответ 41,7%.
Ответ: 41,7
Задание №3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
Решение:
Для ответа на вопрос задания необходимо сравнить две площади – посевную площадь до строительства террас и площадь террас.
Посевная площадь у нас найдена в задании №1, она равна 390 м2.
Требуется найти площадь террас. Надо понять, что она собой представляет. Посмотрим внимательно на рисунок, где изображены террасы («ступеньки» можно их назвать, глядя на рисунок). Если каждую такую «ступеньку» опустить вниз, то они как раз войдут в расстояние 12 м, то есть длина всех террас, отведённых под посевы равна 12 метров. Ширина участка нам известна, она равна 30 метров. Таким образом, мы получили прямоугольник со сторонами 12 и 30 метров, значит, найдем его площадь, что и будет являться площадью террас: 12×30=360 м2.
Вот теперь мы видим, что сначала площадь была 390, а затем она немного уменьшилась и стала равна 360 м2.
Осталось сравнить процентное отношение данных площадей.
Это можно сделать двумя способами.
1 способ: запишем условие для решения, помня, что первоначальная площадь равна 100%.
390 м2 – 100%
360 м2 – х%
Найдем, сколько процентов стала площадь террас: х= 360×100:390=92,307… Так как нам сказано в условии, что ответ надо будет округлить до десятых, то можно это сделать с числом 92,307…: 92,307≈92,3. Помним, что это мы нашли, сколько процентов стала площадь террас. Теперь находим разницу между ними: 100% — 92,3%=7,7%. Её и запишем в ответ.
2 способ: можно решить данную задачу другим способом, имея две площади – 390 м2 и 360 м2. Видим, что площадь уменьшилась на 30 м2, так как 390 – 360 =30.
Значит: 390 м2 – 100%, а 30 м2 — х%. Следовательно х=30×100:390=7,69…%. Округлим до десятых наше число и получим 7,7.
Ответ: 7,7
Задание №4. Земледелец получает 800 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 22% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
Решение:
Смысл данной задачи в том, что земледелец выращивает на террасах бурый рис, затем его обрабатывает и получает белый рис. При обработке масса теряется. Нам надо узнать, сколько кг белого риса он получит со своего участка.
Помним, что рис собирают с террас, площадь которых 360 м2 (мы нашли её в задании 3). Известно, что с 1 м2 собирают 800 г бурого риса, следовательно, чтобы найти, сколько бурого риса он соберет со всего участка площадью 360 м2, надо 800×360, получим 288000 граммов. Переведем граммы в килограммы (это требуется в данной задаче), то есть разделим на 1000, так как 1 кг=1000 г. Значит, 288000:1000=288 кг собирает земледелец бурого риса.
Теперь он его обрабатывает, теряя 22%, значит, из данной массы 288 кг мы должны убрать 22%. Так как 288 кг – это 100%, то после обработки остается 100% — 22%=78%. Переведем 78% в десятичную дробь, получим 0,78. Теперь умножим на 0,78 наши 288 кг, получаем 224,64 кг.
Ответ: 224,64
Задание №5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Рис | Кукуруза | Пшено | |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Решение:
Итак, подчеркнем в условии для себя, что нам надо найти: В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
Наибольшее число килограммов урожая летом – это урожай кукурузы, а осенью – урожай риса. Выделим это в таблице:
| Рис | Кукуруза | Пшено | |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Складываем эти два числа: 1200+800=2000 г/м2, получаем количество урожая с 1 квадратного метра в граммах. Знаем, что площадь террас равна 360 м2 (мы нашли её в задании номер 3). Значит, надо 2000 умножить на 360, получим: 2000×360=720000 г/м2. Теперь переведем наше число в килограммы, так как это требуется по условию задачи: 720000 г = 720 кг (знаем, что 1 кг=1000 г, поэтому разделили на 1000, убрав три нуля). Наш ответ 720 кг
Ответ: 720
Ответ: см. решение
Спасибо за разбор, все очень подробно и понятно?