Задание EF17513
📜Теория для решения: Сила трения Динамика движения по окружности с постоянной по модулю скоростью
Посмотреть решение
Алгоритм решения
Решение
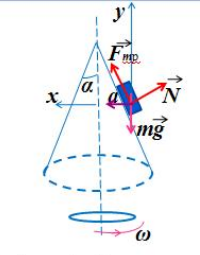
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
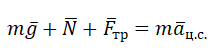
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
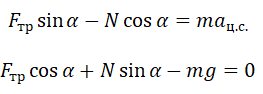
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
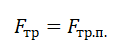
Максимальное значение силы трения равно:
![]()
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
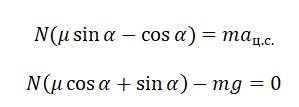
Запишем систему уравнение в следующем виде:
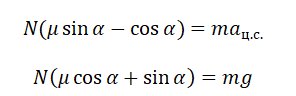
Поделим первое уравнение на второе и получим:
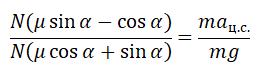
Сделаем сокращения и получим:
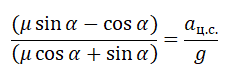
Отсюда центростремительное ускорение равно:
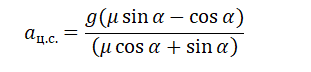
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
![]()
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
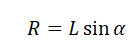
Отсюда центростремительное ускорение равно:
![]()
Выразим искомую величину L:
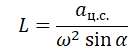
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
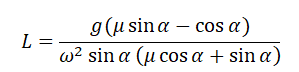
Поделим числитель на синус угла α, чтобы упростить выражение, и получим: