Задание EF18057 • СПАДИЛО

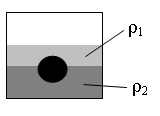На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ₁ = 400 кг/м³ и ρ₂ = 2ρ₁, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?

📜Теория для решения: Архимедова сила

Посмотреть решение

Алгоритм решения

1.Записать исходные данные.

2.Выполнить рисунок.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в проекции на ось ординат.

5.Выполнить общее решение.

6.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Плотность первой жидкости: ρ₁ = 400 кг/м³.

• Плотность второй жидкости: ρ₂ = 2ρ₁.

• Объем шарика: V.

• Объем шарика выше границы раздела двух жидкостей: V₁ = V/4.

• Объем шарика выше границы раздела двух жидкостей: V₂ = 3V/4.

Построим рисунок и укажем все силы, действующие на шарик:

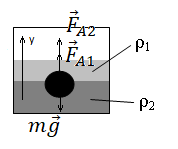
Запишем второй закон Ньютона в векторном виде:

$m \to g + {\to F}_{A 1} + {\to F}_{A 2} = 0$

Запишем второй закон Ньютона в виде проекции на ось ординат:

$m g = F_{A 1} + F_{A 2}$

Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:

$ρ V g = ρ_{1} g V_{1} + ρ_{2} g V_{2}$

Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:

$ρ V = \frac{ρ_{1} V}{4} + \frac{2 ρ_{1} 3 V}{4}$

Объемы сокращаются. Остается:

$ρ = \frac{ρ_{1}}{4} + \frac{2 ρ_{1} 3}{4} = \frac{7 ρ_{1}}{4} = \frac{7 \cdot 400}{4} = 700 (\frac{к г}{м^{3}})$

Ответ: 700

Текст: Алиса Никитина, 1.2k 👀