Задание EF18982
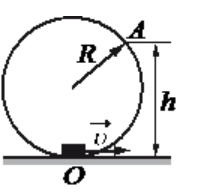 Небольшая шайба массой m=10 г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14 м, скользит по его внутренней поверхности. На высоте h=0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок с указанием сил, действующих на шайбу в точке А.
Небольшая шайба массой m=10 г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14 м, скользит по его внутренней поверхности. На высоте h=0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок с указанием сил, действующих на шайбу в точке А.
📜Теория для решения: Динамика движения по окружности с постоянной по модулю скоростью
Посмотреть решение
Алгоритм решения
Решение
Запишем исходные данные:
Сделаем чертеж. Выберем систему координат такую, чтобы направление линейной скорости шайбы в точке совпадала с направлением оси ОУ.
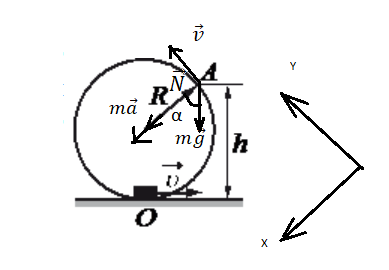
Запишем второй закон Ньютона в векторной форме:
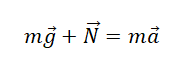
Под ускорением в этой записи понимается полное ускорение, составляющими которого является центростремительное и тангенциальное ускорение, направленное касательно к окружности (на рисунке мы его не обозначили, так как оно нам не понадобится).
Запишем проекцию на ось ОХ. Учтем, что в точке А шайба отрывается от кольца и падает. Следовательно, нормальная реакции опоры равна нулю:
mg cosα = maц.с.
Кинетическая энергия тела определяется формулой:
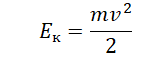
Выразим центростремительное ускорение из проекции на ось ОХ:
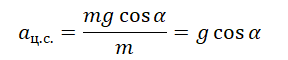
Но центростремительное ускорение также определяется формулой:
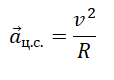
Приравняем правые части уравнений и получим:
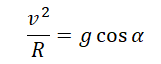
Квадрат скорости будет равен:
![]()
Следовательно, кинетическая энергия равна:
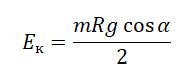
Чтобы избавиться от неизвестных величин, обратимся к геометрии:
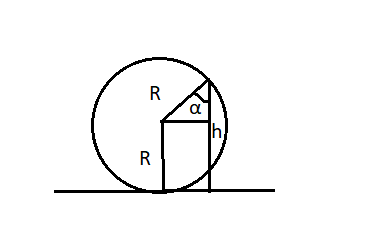
Из рисунка видно, что высота h есть сумма радиуса окружности и произведения радиуса на косинус угла α:
h = R + Rcosα
Отсюда следует, что:
Rcosα = h – R
Подставим это выражение в формулу кинетической энергии и выполним вычисления:
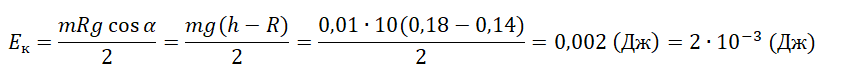
Отсюда следует, что кинетическая энергия шарика в начале движения равна 2 мДж.