Задание OM1806o • СПАДИЛО

Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 41°. Ответ дайте в градусах.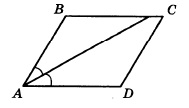

📜Теория для решения:

Посмотреть решение

Так как АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х. Поскольку АВСD параллелограмм, то ∠В+∠А=180°. Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=180°–2х. Рассмотрим ∆АВК:

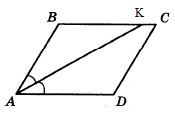
По теореме о сумме углов треугольника ∠ВАК+∠В+∠ВКА=180°

По условию ∠ВКА = 41°

Отсюда получаем:

х+ 180°–2х+41⁰=180°

х–2х=180⁰–180⁰–41°

–х=–41°

х=41°

Значит, искомый (острый) ∠А=2·41⁰=82°

Ответ: 82

Текст: Базанов Даниил, 1k 👀