Задание OM1802o
📜Теория для решения:
Посмотреть решение
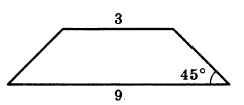
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
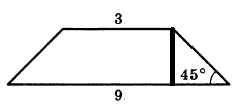
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.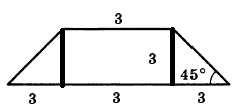
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
( 9 — 3 ) / 2 = 3
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Ответ: 18