Задание EF18127 • СПАДИЛО

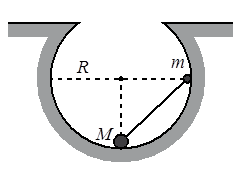Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.

В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?

📜Теория для решения: Закон сохранения механической энергии

Посмотреть решение

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.

3.Записать закон сохранения энергии.

4.Выполнить общее решение задачи.

5.Подставить известные данные и выполнить вычисление искомой величины.

Решение

Запишем исходные величины:

• Масса первого шарика: m = 30 г.

• Масса второго шарика: M = 60 г.

• Максимальная высота подъема шарика М: H = 12 см.

Переведем единицы измерения величин в СИ:

30 г = 0,03 кг

60 г = 0,06 кг

12 см = 0,12 м

Выполним чертеж:

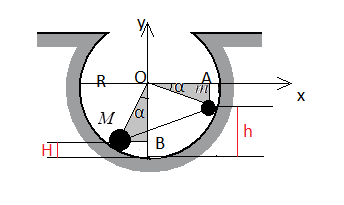
Нулевой уровень — нижняя точка выемки.

Запишем закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p= const

В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:

E_p0m= mgR

Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:

E_pm= mgh

E_pM= MgH

Поэтому закон сохранения энергии применительно к задаче примет вид:

mgR = mgh + MgH

Преобразуем выражение и получим:

$m g R - m g h = M g H$

$R - h = \frac{M g H}{m g} = \frac{M H}{m}$

При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:

MB = mA = R – h

OA = OB = R – H

OM = Om = R

Это дает нам право воспользоваться теоремой Пифагора:

${(R - h)}^{2} = R^{2} - {O A}^{2} = R^{2} - {(R - H)}^{2}$

Следовательно:

${(R - h)}^{2} = R^{2} - (R^{2} - 2 R H + H^{2}) = 2 R H - H^{2}$

Подставим в это выражение правую часть ранее полученного выражения: $.$

$R - h = \frac{M H}{m}$

${(\frac{M H}{m})}^{2} = 2 R H - H^{2}$

Теперь можем выразить и вычислить радиус:

$2 R H = {(\frac{M H}{m})}^{2} + H^{2}$

$R = \frac{{(\frac{M H}{m})}^{2} + H^{2}}{2 H}$

$R = {(\frac{M}{m})}^{2} \frac{H}{2} + \frac{H}{2} = {(\frac{0, 06}{0, 03})}^{2} \frac{0, 12}{2} + \frac{0, 12}{2} = 0, 3 (м)$

Ответ: 0,3

Текст: Алиса Никитина, 1.5k 👀